Bài 3.4, 3.5, 3.6, 3.7 trang 42 SBT Toán 7 tập 2
Bài 3.4, 3.5, 3.6, 3.7 trang 42 SBT Toán 7 tập 2
Bài 3.4: Hãy tìm cạnh của tam giác cân, nếu hai cạnh của nó bằng
a) 7cm và 3cm ;
b) 8cm và 2cm ;
c) 10cm và 5cm;
Lời giải:
a) Vì 3 + 3 < 7 nên tam giác cân đó có cạnh bên bằng 7cm và cạnh đáy bằng 3cm
b) Cạnh bên bằng 8cm và cạnh đáy bằng 2cm.
c) Cạnh bên bằng 10cm và cạnh đáy bằng 5cm.
Bài 3.5: Chứng minh rằng trong một đường tròn, đường kính là dây lớn nhất.
Lời giải:
Giả sử CD là một dây của đường tròn bán kính R và AB là một đường kính của nó. Ta có:
- Nếu C, O, D không thẳng hàng thì trong tam giác COD có
CD < OC + OD = 2R = AB.
- Nếu C, O, D thằng hàng thì
CD = OC + OD = 2R = AB
Vậy trong mọi trường hợp ta luôn có đường kính là dây lớn nhất.
Bài 3.6: Chứng minh “Bất đẳng thức tam giác mở rộng ”: Với ba điểm A, B, C bất kỳ, ta có AB + AC ≥ BC
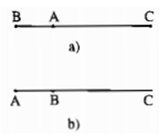
Lời giải:
- Nếu A, B, C không thẳng hàng thì trong tam giác ABC ta có AB + AC > BC
- Nếu A, B, C thẳng hàng và A ở giữa B và C hoặc trùng B, C thì AB + AC = BC
Vậy với ba điểm A, B, C bất kỳ ta luôn có AB + AC ≥ BC
Bài 3.7: Cho đường thẳng d và hai điểm A, B nằm cùng một phía của d và AB không song song với d. Một điểm M di động trên d. Tìm vị trí của M sao cho |MA − MB| là lớn nhất
Lời giải:
Vì AB không song song với d nên AB cắt d tại N.
Với điểm M bất kỳ thuộc d mà M không trùng với N thì ta có tam giác MAB.
Do đó
|MA − MB| < AB
Khi M ≡ N thì
|MA − MB| = AB
Vậy |MA − MB| lớn nhất là bằng AB, khi đó M ≡ N là giao điểm của hai đường thẳng d và AB.

