Bài 38, 39, 40 trang 25 SBT Toán 7 tập 2

Bài 38, 39, 40 trang 25 SBT Toán 7 tập 2

Bài 38: Tính f(x) + g(x) với:

f(x) = x⁵ – 3x² + x³ – x² – 2x + 5

g(x) = x² – 3x + 1 + x² – x⁴ + x⁵

Lời giải:

Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:

* Ta có: f(x) = x⁵ – 3x² + x³ – x² – 2x + 5 = x⁵ + x³ – 4x² – 2x + 5

g(x) = x² – 3x + 1 + x² – x⁴ + x⁵ = x⁵ – x⁴ + 2x² – 3x + 1

* f(x) + g(x):

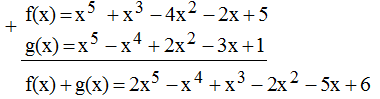
Bài 39: Tính f(x) – g(x) với:

f(x) = x⁷ – 3x² – x⁵ + x⁴ – x² + 2x – 7

g(x) = x – 2x² + x⁴ – x⁵ – x⁷ – 4x² – 1

Lời giải:

Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:

* Ta có: f(x) = x⁷ – 3x² – x⁵ + x⁴ – x² + 2x – 7

            = x⁷ – x⁵ + x⁴ – 4x² + 2x - 7

g(x) = x – 2x² + x⁴ – x⁵ – x⁷ – 4x² – 1

            = -x⁷ – x⁵ + x⁴ – 6x² + x – 1

* f(x) – g(x)

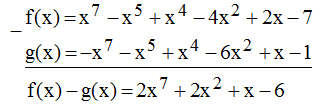
Bài 40: Cho các đa thức:

            f(x) = x⁴ – 3x² + x – 1

            g(x) = x⁴ – x³ + x² + 5

a. Tìm h(x) biết f(x) + h(x) = g(x)

b. Tìm h(x) biết f(x) – h(x) = g(x)

Lời giải:

a. Ta có: f(x) + h(x) = g(x)

Suy ra: h(x) = g(x) – f(x) = (x⁴ – x³ + x² + 5) – (x⁴ – 3x² + x – 1)

            = x⁴ – x³ + x² + 5 – x⁴ + 3x² – x + 1

            = -x³ + 4x² – x + 6

b. Ta có: f(x) – h(x) = g(x)

Suy ra: h(x) = f(x) – g(x) = (x⁴ – 3x² + x – 1) – (x⁴ – x³ + x² + 5)

            = x⁴ – 3x² + x – 1 – x⁴ + x³ – x² – 5

            = x³ – 4x² + x – 6