Bài 6.4, 6.5 trang 149 SBT Toán 7 tập 1

Bài 6.4, 6.5 trang 149 SBT Toán 7 tập 1

Bài 6.4: Cho hình bs 4. Chứng minh rằng :

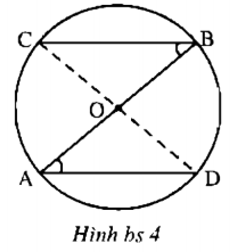
a) C,O,D thẳng hàng ;

b) BC = AD

Lời giải:

a) Các tam giác cân AOD, BOC có góc ở đáy bằng nhau nên góc ở đỉnh bằng nhau ∠AOD = ∠BOC. Ta lại có ∠AOD + ∠BOD = 180° nên ∠BOC + ∠BOD = 180°.

Vậy C, O, D thẳng hàng.

b) ΔBOC = ΔAOD (g.c.g), suy ra BC = AD.

Bài 6.5: Cho tam giác ABC vuông tại A, ∠B = 30°. Chứng minh rằng AC = (1/2)BC.

Lời giải:

Lấy điểm D trên cạnh BC sao cho ∠CAD = 60°. Tam giác ACD có ∠A₁ = 60°, ∠C = 60° nên là tam giác đều, suy ra AC = AD = DC.     (1)

Tam giác ABD có ∠A₂ = ∠B (cùng bằng 30°) nên là tam giác cân, suy ra AD = BD.     (2)

Từ (1) và (2) suy ra AC = DC = BD, tức là AC = 1/2BC.