Bài 67, 68, 69, 70, 71, 72, 73, 74, 75, 76 trang 147 SBT Toán 7 tập 1

---

Bài 67, 68, 69, 70, 71, 72, 73, 74, 75, 76 trang 147 SBT Toán 7 tập 1

Bài 67: a, Tính góc ở đáy của một tam giác cân biết góc ở đỉnh bằng 50°,bằng a°.

b, Tính góc ở đỉnh của một tam giác cân biết góc ở đáy bằng 50°,bằng a°

Lời giải:

Vì tam giác cân có hai gốc ở đáy bằng nhau nên số đo của mỗi góc bằng 180o trừ góc ở đỉnh rồi chia cho 2.

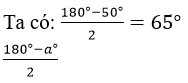
Vì tam giác cân có hai góc ở đáy bằng nhau nên góc ở đỉnh bằng 180otrừ đi hai lần góc ở đáy.

Ta có: 180° - 50°.2 = 180° - 100° = 80°

180° - a.2

Bài 68: Cho tam giác ABC cân tại A có ∠A = 100°. Lấy điểm M thuộc cạnh AB, điểm N thuộc cạnh AC sao cho AM = AN. Chứng minh rằng MN // BC

Lời giải:

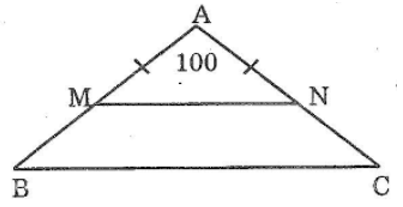
Vì ΔABC cân tại A nên ∠B = ∠C

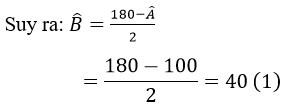
Mà AM = AN (gt) nên ΔAMN cân tại A ⇒ ∠AMN = ∠ANM

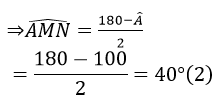
Từ (1) và (2) suy ra: ∠ B = ∠AMN

Vậy MN // BC (vì có cặp góc ở vị trí đồng vị bằng nhau)

Bài 69: Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB.

Chứng minh rằng BM = CN

Lời giải:

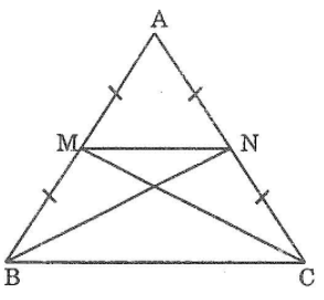
Xét ΔABM và ΔCAN, ta có:

AB = AC (gt)

∠A chung

AM = AN (cùng bằng một nửa AB, AC)

Suy ra: ΔABM = ΔCAN(c.g.c)

Vậy DM = CN ( hai cạnh tương ứng)

Bài 70: Cho tam giác ABC cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH = AK. Gọi O là giao điểm của BH và CK.

Chứng minh rằng ΔOBC là tam giác cân.

Lời giải:

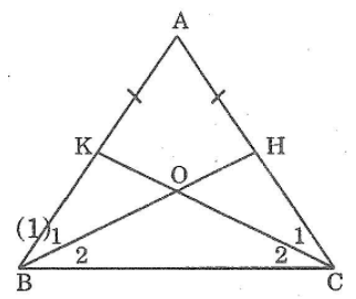
Xét ΔABH và ΔACK, ta có:

AB = AC (gt)

A chung

AH = AK (gt)

Suy ra: ΔABH = ΔACK(c.g.c)

⇒ B₁ = C₁ (hai góc tương ứng)     (1)

∠ABC = B₁ + B₂     (2)

∠ACB = C₁ + C₂     (3)

∠ABC = ∠ACB (tính chất tam giác cân)     (4)

Từ (1),(2),(3) và (4) suy ra: B₂ = C₂ hay ΔBOC cân tại O

Bài 71: Vẽ lại hình bên vào vở rồi đặt bài toán vẽ tam giác để có hình bên.

Lời giải:

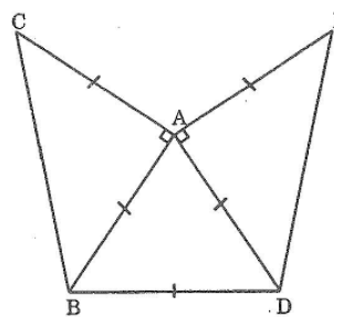
- Vẽ tam giác ABC vuông tại A

- Vẽ tam giác đều ABD sao cho D và C nằm trên 2 nửa mặt phẳng đối nhau có bờ chứa đường thẳng AB.

- Vẽ tam giác vuông cân ADE sao cho E và B nằm trên 2 nửa mặt phẳng đối bờ chứa đường thẳng AD.

Bài 72: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh rằng ΔADE là tam giác cân.

Lời giải:

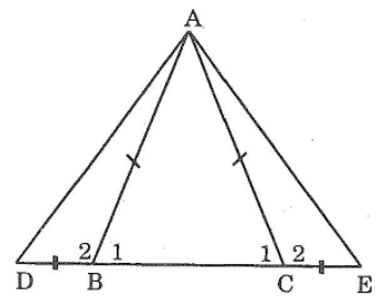
Ta có: ΔABC cân tại A

Suy ra:B₁ = C₁ (tính chất tam giác cân)

Lại có:B₁ + B₂ = 180° (kề bù)

C₁ + C₂ = 180° (kề bù)

Suy ra: C₁ = B₁

Xét ΔABD và ΔACE, ta có:

AB = AC (gt)

C₁ = B₂ (chứng minh trên)

BD = CE (gt)

Suy ra: ΔABD = ΔACE(c.g.c)

⇒ AD = AE ( hai cạnh tương ứng)

Vậy ΔADE cân tại A (theo định nghĩa tam giác cân)

Bài 73: Cho tam giác ABC. Tia phân giác của góc B cắt AC ở D. trên tia đối của tia BA lấy E sao cho BE = BC. Chứng minh rằng BD // EC

Lời giải:

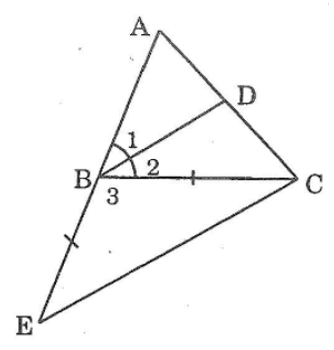
Ta có: BD là tia phân giác của ∠ABC (gt)

Suy ra:B₁ = B₂ = (1/2)ABC

Lại có: BE = BC (gt)

⇒ ΔBEC cân tại B (theo định nghĩa)

∠E = ∠BCE (tính chất tam giác cân)

ΔBEC có ABC là góc ngoài đỉnh B

⇒ ∠ABC = ∠E + ∠BCE (tính chất góc ngoài tam giác)

Suy ra: ∠ABC = 2∠E

Hay ∠E = ∠B₁ = (1/2)∠ABC

Vậy BD // CE (vì có cặp góc ở vị trí đồng vị bằng nhau)

Bài 74: Tính số đo các góc của tam giác ACD như hình bên.

Lời giải:

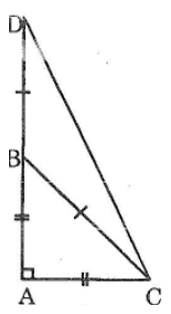
Ta có: ΔABC vuông cân tại A

Suy ra: ∠ACB = ∠ABC = 45°

Lại có: ΔBCD vuông cân tại B (BC = BD)

Suy ra: ∠BCD = ∠Dtính chất tam giác cân)

Trong ΔBCD ta có ∠ABC góc ngoài tại đỉnh B

Do vậy: ∠ABC = ∠BCD + ∠D (tính chất góc ngoài của tam giác)

Suy ra: ∠ABC = ∠2BCD

⇒ ACD = ∠ACB + ∠BCD = 45° + 22°30' = 67°30'

Bài 75: Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Tính số đo góc BCD

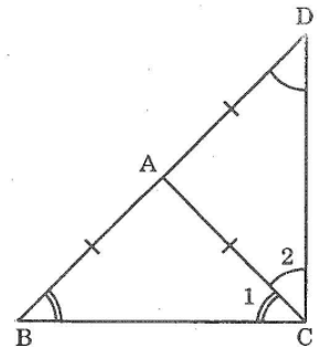
Lời giải:

Ta có: ΔABC cân tại A

⇒ B = C₁ (tính chất tam giác cân)

Lại có: AD = AB (gt)

Suy ra: AD = AC do đó ΔACD cân tại A

∠D = ∠C₂ (tính chất tam giác cân)

Mà ∠BCD = ∠C₁ + C₂

Nên ∠BCD = ∠B + ∠D     (1)

Trong ΔBCD, ta có:

∠BCD + ∠B + ∠D = 180° (tổng 3 góc trong tam giác)     (2)

từ (1)và (2)suy ra : 2 ∠BCD = 180° hay∠BCD = 90°

Bài 76: Cho tam giác ABC cân tại A có cạnh bên bằng 3cm. Gọi D là một điểm thuộc đáy BC. Qua D, kẻ cac đường thẳng song song vói các cạnh bên, chúng cắt AB và AC theo thứ tự tại F và E.

Tính tổng DE + DF

Lời giải:

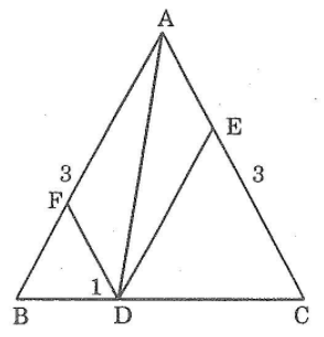
Ta có: DF // AC(gt)

⇒ D₁ = C (hai góc đồng vị)     (1)

Lại có: ΔABC cân tại A

⇒ B = C (tính chất tam giác cân)     (2)

Từ (1) và (2) suy ra: B = D1

Hay ΔBFD caab tại F ⇒ BF = DF

Nối AD. Xét ΔAFD và ΔDEA có:

∠ADF = ∠EAD (so le trong vì DF // AC)

AD cạnh chung

∠FDA = ∠EDA (so le tronh vì DE // AB)

Suy ra: ΔAFD = ΔDEA (g.c.g)

AF = DF (hai cạnh tương ứng)

Vậy: DE + DF = AF + BF = AB = 3cm