Bài 77, 78, 79, 80, 81 trang 148 SBT Toán 7 tập 1

Bài 77, 78, 79, 80, 81 trang 148 SBT Toán 7 tập 1

Bài 77: Cho tam giác đều ABC. Lấy các điểm D, E , F theo thứ tựu thuộc các cạnh B. BC và cA sao cho AD = BE = CF. Chứng minh rằng tam giác DEF là tam giác đều?

Lời giải:

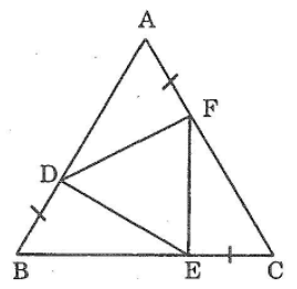
Ta có: AB = AD +DB     (1)

BC = BE = EC     (2)

AC = AF + FC     (3)

AB = AC = BC     (4)

AD = BE = CF     (5)

Từ (1), (2), (3) và (4),(5) suy ra: BD = EC = AF

Xét ΔADF và ΔBED, ta có:

AD = BE (gt)

∠A = ∠B = 60° (vì tam giác ABC đều)

AE = BD (chứng minh trên)

suy ra: ΔADF = ΔBED (c.g.c)

DF = ED (hai cạnh tương ứng)     (6)

Xét ΔADF và ΔCFE, ta có:

AD = CF (gt)

∠A = ∠C = 60° (vì tam giác ABC đều)

EC = AF (chứng minh trên)

suy ra: ΔADF = ΔCFE (c.g.c)

DF = FE (hai cạnh tương ứng)     (7)

Từ (6) và (7) suy ra: DF – ED = FE

Vậy tam giác DFE đều

Bài 78: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. qua I kẻ đường thẳng song song với BC. Gọi giao điểm của đường thẳng này với AB, AC theo thứ tự là D,E.

Chứng minh rằng: DE = BD + CE

Lời giải:

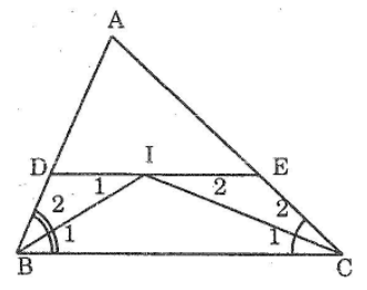
Ta có: DI // BC (gt)

Suy ra:∠I₁ = ∠B₁ (so le trong)     (1)

Lại có:∠B₁ = ∠B₂     (2)

(vì BI là tia phân giác góc B)

Từ (1) và (2) suy ra:∠I₁ = ∠B₂

⇒ ΔBDI cân tại D ⇒ BD = DI     (3)

Mà IE // BC (gt) ⇒ ∠I₁ = ∠C₁ (so le trong)     (4)

Đồng thời: ∠C₁ = ∠C₂ (vì CI là phân giác của góc C)     (5)

Từ (4) và (5) suy ra: ∠C₁ = ∠C₂. Suy ra. ∠CEI cân tại E

Suy ra: CE = EI (hai cạnh tương ứng)     (6)

Từ (3) và (6) suy ra: BD + CE = DI + EI = DE

Bài 79: Cho đường tròn tâm O đường kính AB. Gọi M là điểm nằm trên đường tròn, tính số đo góc AMB.

Lời giải:

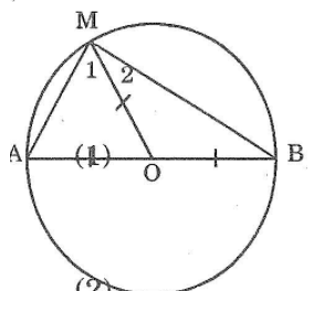
Nối OM, ta có:

OA = OM (bán kính đường tròn tâm O)

Nên ΔOAM cân tại O

⇒ ∠A = ∠M₁ (tính chất tam giác cân)     (1)

OM = OB (bán kính đường tròn tâm O)

Suy ra: ΔOBM cân tại O

⇒ ∠B = ∠M₂ (tính chất tam giác cân)     (2)

Trong ΔAMB ta có:

∠A = ∠AMB = ∠B = 180 (tổng ba góc trong tam giác)

⇒ ∠A + ∠B + ∠M₁ + ∠M₂ = 180°     (3)

Từ (1), (2) và (3) suy ra: 2(M₁ + M₂) = 180°

Vậy:

(∠M₁ + ∠M₂) = 90° hay (AMB) = 90°

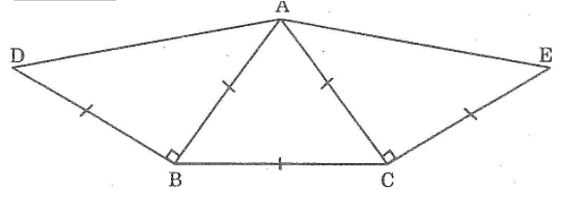
Bài 80: Đặt đề toán theo hình dưới đây. Sau đó vẽ lại hình theo đề toán rồi đo goác DAE

Lời giải:

Đề toán:

Vẽ tam giác ABC đều

Vẽ tam giác ABD vuông cân tại B sao cho D và C nằm trên hai nửa mặt phẳng bờ chứa đường thẳng AB.

Vẽ tam giác ACE vuông cân tại C sao cho E và B nằm trên hai nửa mặt phẳng đối có bờ chứa đường thẳng AC

Đo ∠DAE = 150°

Chứng minh:

∠DAE = ∠DAB + ∠BAC + ∠CAE = 45° + 60° + 45° = 150°

Bài 81: Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình dưới ) là tam giác nhọn.

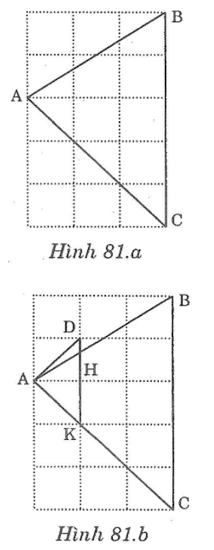
Lời giải:

Nối A với D tạo tành đường chéo ô vuông

Gọi K giao điểm AC với đỉnh ô vuông, H là giao điểm DK với đường kẻ ô vuông từ A.

Ta có: ΔAHK vuông cân tại H ⇒ ∠HAK = 45°

ΔAHD vuông cân tại H⇒ ∠HAD = 45°

⇒ ∠DAK = ∠HAK + ∠HAD = 45° + 45° = 90°

hay ∠DAC = 90°

⇒ ∠BAC < 90°

Trên hình vẽ: ∠ACB < 90° và ∠ABC < 90°

Vậy tam giác ABC là tam giác nhọn