Bài 54, 55, 56, 57 trang 47 SBT Toán 7 tập 2
Bài 54, 55, 56, 57 trang 47 SBT Toán 7 tập 2
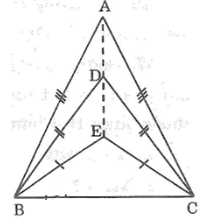
Bài 54: Cho ba tam giác cân ABC, DBC, EBC chung đáy BC. Chứng minh rằng ba điểm A, D, E thẳng hàng.
Lời giải:
Tam giác ABC cân tại A nên AB = AC
Khi đó A thuộc đường trung trực của BC (1)
Tam giác DBC cân tại D nên DB = DC
Khi đó D thuộc đường trung trực của BC (2)
Tam giác EBC cân tại E nên EB = EC
Khi đó E thuộc đường trung trực của BC (3)
Từ (1), (2) và (3) suy ra: A, D, E thẳng hàng.
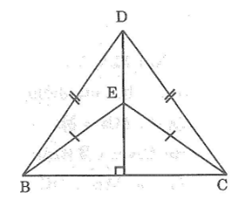
Bài 55: Cho hai điểm D, E nằm trên đường trung trực của đoạn thẳng BC. Chứng minh rằng ΔBDE = ΔCDE.
Lời giải:
Vì D thuộc đường trung trực của BC nên DB = DC (tính chất đường trung trực)
Vì E thuộc đường trung trực của BC nên EB = EC (tính chất đường trung trực)
Xét ΔBDE và ΔCDE, ta có:
DB = DC (chứng minh trên)
DE cạnh chung
EB = EC (chứng minh trên)
Suy ra: ΔBDE = ΔCDE (c.c.c).
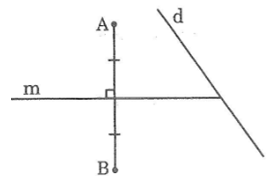
Bài 56: Cho đường thẳng d và hai điểm A, B thuộc cùng một nửa mặt phẳng có bờ d. Tìm một điểm C nằm trên d sao cho C cách đều A và B.
Lời giải:
* Nếu AB không vuông góc với d
- Vì điểm C cách đều hai điểm A và B nên C nằm trên đường trung trực của AB.
- Điểm C ∈ d
Vậy C là giao điểm của đường trung trực của AB và đường thẳng d.
Cần dựng đường thẳng m là đường trung trực của đoạn thẳng AB cắt đường thẳng d tại C.
Vậy C là điểm cần tìm.
* Nếu AB vuông góc với d
Khi đó đường trung trực của AB song song với đường thẳng d nên không tồn tại điểm C.
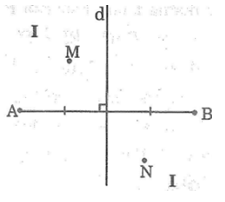
Bài 57: Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần I và II như hình dưới. Cho điểm M thuộc phần I và điểm N thuộc phần II. Chứng minh rằng:
a. MA < MB
b. NA > NB
Lời giải:
a. Nối MA, MB
Gọi C là giao điểm của MB với đường thẳng d, nối CA
Ta có: MB = MC + CB
Mà CA = CB (tính chất đường trung trực)
Suy ra: MB = MC + CA (1)
Trong ΔMAC, ta có:
MA < MC + CA (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra: MA < MB
b. Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB
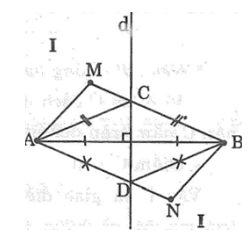
Ta có: NA = ND + DA
Mà DA = DB (tính chất đường trung trực)
Suy ra: NA = ND + DB (3)
Trong ΔNDB, ta có: NB < ND + DB
(bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA > NB.

