Bài 58, 59, 60, 61, 62, 63 trang 48 SBT Toán 7 tập 2

Bài 58, 59, 60, 61, 62, 63 trang 48 SBT Toán 7 tập 2

Bài 58: Cho hình bên. Chứng minh rằng AB vuông góc với CD.

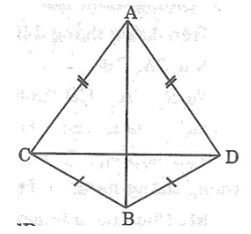
Lời giải:

Vì AC = AD (gt) nên A thuộc đường trung trực của CD.

Vì BC = BD (gt) nên B thuộc đường trung trực của CD.

Vì A ≠ B nên AB là đường trung trực của CD.

Vậy AB ⊥ CD.

Bài 59: Cho hai điểm A, B và một đường thẳng d. Vẽ đường tròn tâm O đi qua hai điểm A, B sao cho O nằm trên đường thẳng d.

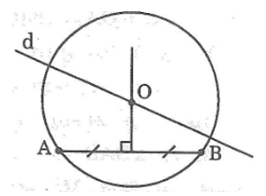
Lời giải:

- Vì A và B là hai điểm nằm trên đường tròn tâm O nên OA = OB.

- Suy ra O thuộc đường trung trực của đoạn AB.

Vì tâm O nằm trên đường thẳng d nên O là giao điểm của đường trung trực của AB và đường thẳng d.

- Dựng đường thẳng m là đường trung trực của AB cắt d tại O.

- Vẽ đường tròn tâm O bán kính OA (hoặc OB).

* Lưu ý:

- Nếu m // d thì không dựng được tâm O

- Nếu m trùng với d thì có vô số điểm chung O do đó có vô số đường tròn thỏa mãn bài toán.

Bài 60: Cho đoạn thẳng AB. Tìm tập hợp các điểm C sao cho tam giác ABC là tam giác cân có đáy là AB.

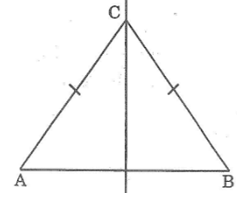
Lời giải:

* Chứng minh thuận

Vì ΔCAB cân tại C nên CA = CB

Suy ra C thuộc đường trung trực của AB

Vì điểm C thay đổi mà ΔCAB luôn cân tại C nên C nằm trên đường trung trực của đường thẳng AB.

* Chứng minh đảo

Trên đường thẳng d lấy điểm C bất ký (C khác trung điểm M của AB).

Nối CA, CB.

Ta có: CA = CB (tính chất đường trung trực)

Suy ra tam giác CAB cân tại C.

Tập hợp các điểm C có tính chất CA = CB và ba điểm A, B, C không thẳng hàng là đường trung trực của AB.

Bài 61: Cho góc xOy bằng 60°, điểm A nằm trong góc xOy. Vẽ điểm B sao cho Ox là đường trung trực của AB. Vẽ điểm C sao cho Oy là đường trung trực của AC.

a. Chứng minh rằng OB = OC.

b. Tính số đo góc BOC.

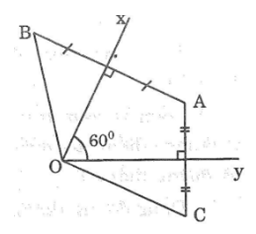
Lời giải:

a. Vì Ox là đường trung trực của AB nên:

OB = OA (t/chất đường trung trực)    (1)

Vì Oy là đường trung trực của AC nên:

OA = OC (t/chất đường trung trực)    (2)

Tư (1) và (2) suy ra: OB = OC.

b. Vì ΔOAB cân tại O và Ox là đường trung trực của AB nên Ox là đường phân giác của ∠(AOB) (tính chất tam giác cân)

Suy ra: ∠O₃ = ∠O₄    (3)

Vì tam giác OAC cân tại O và Oy là đường trung trực của AC nên Oy là đường phân giác của ∠(AOC) (tính chất tam giác cân)

Suy ra: ∠O₁ = ∠O₂    (4)

Từ (3) và (4) suy ra: ∠O₁ + ∠O₃ = ∠O₂ + ∠O₄

Ta có: ∠(BOC) = ∠O₁ + ∠O₃ + ∠O₂ + ∠O₄

= 2(∠O₁ + ∠O₃ ) = 2.(xOy) = 2.60° = 120°.

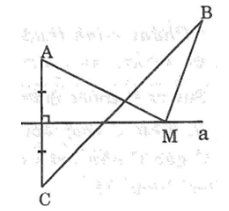
Bài 62: Cho hình bên, M là một điểm tùy ý nằm trên đường thẳng a. Vẽ điểm C sao cho a là đường trung trực của AC.

a. Hãy so sánh MA + MB với BC.

b. Tìm vị trí của điểm M trên đường thẳng a để MA + MB là nhỏ nhất.

Lời giải:

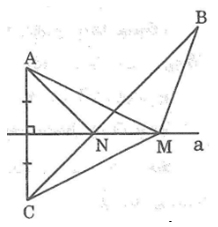
a. Gọi N là giao điểm của BC với đường thẳng a.

* Nếu M ≠ N

Nối MC.

Vì a là đường trung trực của AC nên M ∈ a

Suy ra: MA = MC (tính chất đường trung trực)    (1)

Trong ΔMBC, ta có:

BC < MB + MC (bất đẳng thức tam giác)    (2)

Thay (1) vào (2) ta có: BC < MA + MB

* Nếu M trùng với N

Nối NA. Ta có:

NA = NC (tính chất đường trung trực)

Mà: MA + MB = NA + NB = NC + NB = BC

Vậy: MA + MB ≥ BC.

b. Theo chứng minh trên, khi M trùng với N thì MA + MB = BC bé nhất. Vậy khi M là giao điểm của BC với đường thẳng a thì MA + MB bé nhất.

Bài 63: Hai nhà máy được xây dựng tại hai địa điểm A và B nằm về một phía của khúc sông thẳng. Tìm trên bờ sông một địa điểm C để xây một trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ C đến A và đến B là nhỏ nhất.

Lời giải:

- Dựng điểm A' sao cho bờ sông là trung trực của AA'.

- Nối A'B cắt bờ sông tại điểm C.

Theo kết quả của bài 62 thì C là điểm cần tìm có khoảng cách CA + CB ngắn nhất.