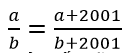Bài 6, 7, 8, 9 trang 6 SBT Toán 7 tập 1

Bài 6, 7, 8, 9 trang 6 SBT Toán 7 tập 1

Bài 6: Chứng minh rằng:

a. Chứng tỏ rằng nếu

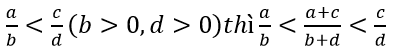
b. Hãy viết 3 số hữu tỉ xen giữa

Lời giải:

a. Ta có:

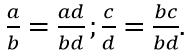
Vì b > 0,d > 0 ⇒ bd > 0

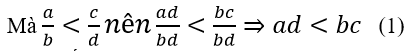
Cộng vào 2 vế của (1) với ab

Suy ra: ad + ab < bc + ab ⇒ a(b + d) < b(a + c)

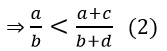
Cộng vào 2 vế của (1) với cd

Suy ra ad + cd < bc + cd ⇒ (a + c)d < c(b + d)

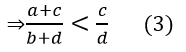
Từ (2) và (3) suy ra:

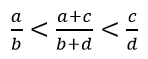
b. Theo câu a ta có:

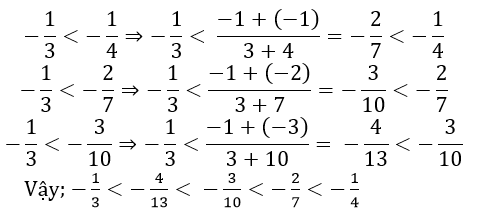
Bài 7: Tìm x ∉ Q , biết rằng x là số âm lớn nhất được viết bằng 3 chữ số 1.

Lời giải:

x = -1/11

Bài 8: So sánh các số hữu tỉ sau bằng cách nhanh nhất:

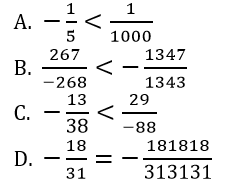
Lời giải:

Bài 9: Cho a, b ∉ Z, b > 0. So sánh 2 số hữu tỉ

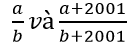
Lời giải:

Ta có: a(b+ 2001) = ab + 2001a

b(a+ 2001) = ab + 2001b

Vì b > 0 nên b + 2002 > 0

a. Nếu a > b thì ab + 2001a > ab + 2001b

⇒ a(b + 2001 ) > b( a + 2001)

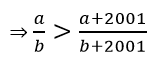
b. Nếu a < b thì ab + 2001a < ab + 2001b

⇒ a(b + 2001 ) < b( a + 2001)

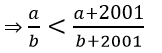
c. Nếu a = b thì