Bài 82, 83, 84, 85, 86, 87 trang 149 SBT Toán 7 tập 1

Bài 82, 83, 84, 85, 86, 87 trang 149 SBT Toán 7 tập 1

Bài 82: Tính cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 13 cm, cạnh góc vuông kia bằng 12 cm

Lời giải:

Giả sử ΔABC có ∠A = 90°, BC = 13 cm, AC = 12cm

Theo định lý pitago ta có: BC² = AB² = AC²

Suy ra: AB² = BC² - AC² = 13² - 12² = 25

Vậy AB = 5 cm

Bài 83: Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AC = 20vm, AH = 12 cm và BH = 5cm

Lời giải:

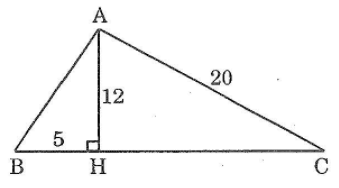
ΔAHB có (AHB) = 90°

Theo định lý pitago, ta có:

AB² = AH² + HB²

= 12² + 5² = 169

Vậy AB = 13 cm

ΔAHC có (AHC) = 90°

Theo định lý pitago, ta có:

AC² = AH² + HC²

HC² = AC² - AH² = 20² - 12² = 400 - 144 = 256

Vậy HC = 16cm

Ta có: BC = BH + HC = 5 +16 = 21cm

Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm

Bài 84: Tính độ dài các đoạn thẳng AB, BC, CD và Da trên hình dưới.

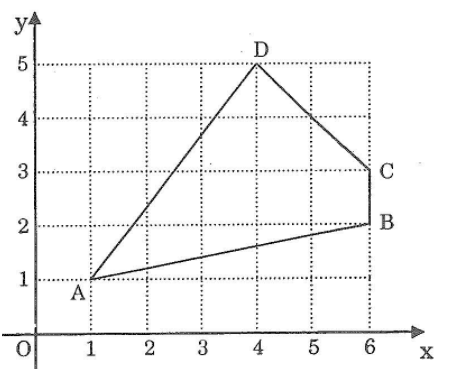
Lời giải:

Theo định lí pitago ta có:

AB² = 5² + 1² = 25 + 1 = 26 ⇒ AB = √26

CD² = 2² + 2² = 4 + 4 = 8 ⇒ CD = √8

AD² = 3² + 4² = 9 + 16 = 25 ⇒ AD = 5

Và BC = 1

Bài 85: Màn hình của một máy thu hình có dạnh hình chữ nhật, chiều rộng 12 inh-sơ, đường chéo 20inh-sơ. Tính chiều dài

Lời giải:

Giả sử màn hình máy thu hình là hình chữ nhật ABCD, chều rộng BC = AD, chiều dài AB = CD, đường chéo AC = BD.

Ta có tam gác ABD vuông tại A

Theo định lí pitago ta có: BD² = AB² + AD²

⇒ AB² = BD² – AD² = 20² - 12² = 400 - 144 = 256

Vậy AB = 16 inh-sơ

Bài 86: Tính đường chéo của một mặt bàn hình chữ nhật có chiều dài 10dm, chiều rộng 5dm

Lời giải:

Giả sử mặt bàn hình chữ nhật ABCD, chiều rộng BC = AD, chiều dài AB = CD, đường chéo AC = BD

Ta có tam giác ABD vuông tại A.

Theo định lí pita go ta có: BD² = AB² + AD²

BD² = 10² + 5² = 100 + 25 = 125

Vậy : BD = √125 = 25dm

Bài 87: Hai đoạn thẳng AC, BD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đoạn thẳng. Tính các độ dài AB,BC,CD,DA biết AC = 12 cm; BD = 16cm

Lời giải:

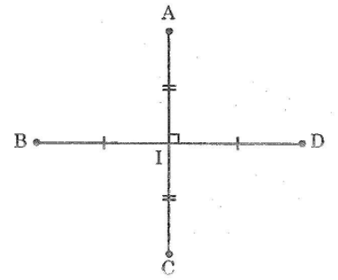
Gọi I là giao điểm của AC và BD

Ta có: IA = IC = AC/2 = 6cm

IB = ID = BD/2 = 8cm

Áp dụng định lí pitago vào tam giác vuông AIB ta có:

AB² = IA² + IB²

AB² = 6² + 8² = 36 + 64 = 100

Vậy AB = 10 cm

Mặt khác: ΔIAB = ΔIAD = ΔICB = ΔICD(c.g.c)

Suy ra: AD = BC = CD = AB = 10cm