Bài 9.1, 9.2, 9.3 trang 95 SBT Toán 8 tập 1

---

Bài 9.1, 9.2, 9.3 trang 95 SBT Toán 8 tập 1

Bài 9.1 trang 95 SBT Toán 8 Tập 1: Một hình chữ nhật có hai cạnh kề bằng nhau 4cm và 6cm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu xentimét ?

A. 8cm

B. √52 cm

C. 9cm

D. √42 cm

Hãy chọn phương án đúng.

Lời giải:

Chọn B

Bài 9.2 trang 95 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Tính số đo góc IHK.

Lời giải:

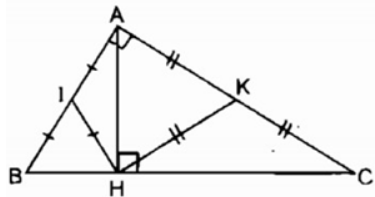
ΔAHB vuông tại H có HI là đường trung tuyến thuộc cạnh huyền AB

⇒ HI = IA = 1/2 AB (tính chất tam giác vuông)

⇒ ΔAH cân tại I

⇒ (IAH) = (IHA) (1)

ΔAHC vuông tại H có HK là đường trung tuyến thuộc cạnh huyền AC

⇒ HK = KA = 1/2 AC (tính chất tam giác vuông)

⇒ ΔKAH cân tại K ⇒∠(KAH) = ∠(KHA) (2)

∠(IHK) = ∠(IHA) + ∠(KHA) (3)

Từ (1), (2) và (3) suy ra: ∠(IHK) = ∠(IAH) + ∠(KAH) = ∠(IAK) = ∠(BAC) = 90^o

Bài 9.3 trang 95 SBT Toán 8 Tập 1: Cho hình thang cân ABCD, đường cao AH. Gọi E, F theo thứ tự là trung điểm của các cạnh bên AD, BC. Chứng minh rằng EFCH là hình bình hành.

Lời giải:

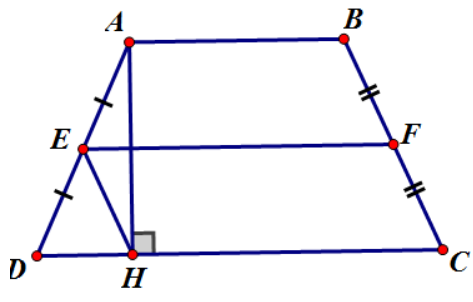
*Có AH ⊥ CD ⇒ ΔAHD vuông tại H

E là trung điểm của AD ⇒ HE là trung tuyến ứng với cạnh huyền AD

⇒ HE = 1/2 AD (1)

*F là trung điểm của AC ⇒ CF = 1/2 BC (2)

Mà ABCD là hình thang cân ⇒ BC = AD (3)

Từ (1), (2) và (3) ta có: HE = CF (*)

*Mặt khác: EH = ED = 1/2 AD (Chứng minh trên)

⇒ ΔEHD cân tại E

⇒ ∠(EHD) = ∠(EDH)

Mà ∠(EDH) = ∠(FCH) (góc đáy hình thang cân)

⇒ ∠(FCH) = ∠(EHD) (cùng bằng ∠(EDH))

⇒EH // FC (2 góc ở vị trí đồng vị bằng nhau) (**)

Từ (*) và (**) ⇒ EFCH là hình bình hành (1 cặp cạnh song song và bằng nhau)