(SGK + SBT) Giải Toán 8 trang 94 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 94 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 94.
(SGK + SBT) Giải Toán 8 trang 94 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
- Toán lớp 8 trang 94 Tập 1 (sách mới):
- Toán lớp 8 trang 94 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 94 (sách cũ)
Bài 111 trang 94 SBT Toán 8 Tập 1: Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
Lời giải:
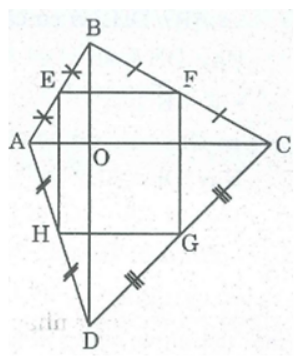
* Trong ΔABC, ta có:
E là trung điểm của AB (gt)
F là trung điểm của BC (gt)
Nên EF là đường trung bình của ΔABC
⇒ EF // AC và EF = 1/2 AC (tính chất đường trung bình tam giác) (1)
* Trong ΔDAC, ta có:
H là trung điểm của AD (gt)
G là trung điểm của DC (gt)
Nên HG là đường trung bình của ΔDAC.
⇒ HG // AC và HG = 1/2 AC (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Ta lại có: BD ⊥ AC (gt)
EF // AC (chứng minh trên)
Suy ra: EF ⊥ BD
Trong ΔABD ta có EH là đường trung bình ⇒ EH // BD
Suy ra: EF ⊥ EH hay (FEH) = 90o
Vậy hình bình hành EFGH là hình chữ nhật.
Bài 112 trang 94 SBT Toán 8 Tập 1: Tìm các hình chữ nhật trong hình vẽ sau.
Lời giải:
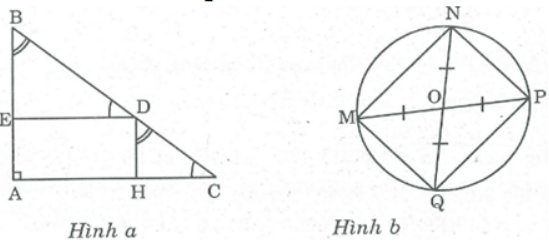
- Hình a ta có:
* ∠B = ∠(HDC)
⇒ AB // DH (vì có cặp góc đồng vị bằng nhau)
Hay DH //AE
* ∠C = ∠(BDE)
⇒ DE // AC (vì có cặp góc đồng vị bằng nhau)
Hay DE //AH
Vậy tứ giác AHDE là hình chữ nhật.
- Hình b: Tứ giác MNPQ có: OM = ON = OP = OQ
⇒ Tứ giác MNPQ có 2 đường chéo cắt nhau tại trưng điểm của mỗi đường và bằng nhau. Vậy MNPQ là hình chữ nhật.
Bài 113 trang 94 SBT Toán 8 Tập 1: Các câu sau đúng hay sai?
a. Hình chữ nhật là tứ giác có tất cả các góc bằng nhau.
b. Tứ giác có hai đường chéo bằng nhau là hình chữ nhật.
c. Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.
Lời giải:
a. Đúng vì hình chữ nhật có 4 góc vuông.
b. Sai vì hình thang cân có 2 cạnh bên không song song có 2 đường chéo bằng nhau.
c. Đúng vì hình chữ nhật có 2 đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Bài 114 trang 94 SBT Toán 8 Tập 1: Cho tam giác ABC vuông cân tại A, AC = 4cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân đường vuông góc kẻ từ M đến AB, AC.
a. Tứ giác ADME là hình gì? Tính chu vi của tứ giác đó.
b. Điểm M ở vị trí nào trên BC thì đoạn DE có độ dài nhỏ nhất.
Lời giải:
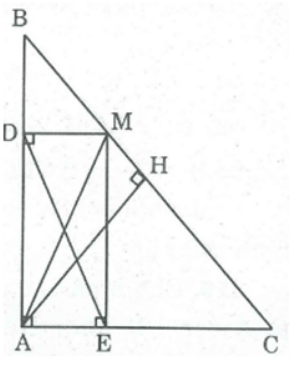
a. Xét tứ giác ADME, ta có:
 = 90o (gt)
MD ⊥ AB (gt)
⇒ ∠(ADM) = 90o
Suy ra tứ giác ADME là hình chữ nhật (vì có 3 góc vuông)
∆ABC vuông cân tại A ⇒ ∠B = 45o
Suy ra: ∆DBM vuông cân tại D
⇒ DM = DB
Chu vi hình chữ nhật ADME bằng:
2(AD + DM) = 2(AD + DB) = 2AB = 2.4 = 8 (cm)
b. Gọi H là trung điểm của BC
Suy ra: AH ⊥ BC (tính chất tam giác cân)
AM ≥ AH (dấu " = " xảy ra khi M trùng với H)
Tứ giác ADME là hình chữ nhật .
⇒ AM = DE (tính chất hình chữ nhật)
Suy ra: DE ≥ AH
Vậy DE = AH có độ dài nhỏ nhất khi và chỉ khi điểm M là trung điểm của BC.
Bài 115 trang 94 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G Gọi D là điểm đối xứng với una M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?
Lời giải:
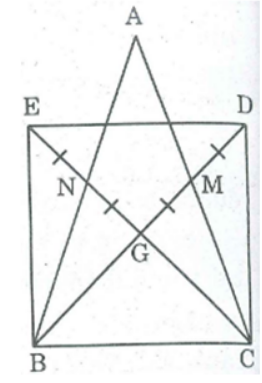
* Ta có: G là trọng tâm của ΔABC .
⇒ GB = 2GM (tính chất đường trung tuyến)
GC = 2GN (tính chất đường trung tuyến)
Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2GM
Suy ra: GB = GD (l)
Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2GN
Suy ra: GC = GE (2)
Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét ΔBCM và ΔCNB, có: BC cạnh chung
∠(BCM) = ∠(CBN) (tính chất tam giác cân)
CM = BN (vì AB = AC)
Suy ra: ΔBCM = ΔCBN (c.g.c)
⇒ ∠B1 = ∠C1 ⇒ ΔGBC cân tại G ⇒ GB = GC ⇒ BD = CE
Hình bình hành BCDE có hai đường chéo bằng nhau nên nó là hình chữ nhật.
Bài 116 trang 94 SBT Toán 8 Tập 1: Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD = 2cm, HB = 6cm. Tính độ dài AD, AB (làm tròn đến hàng đơn vị).
Lời giải:
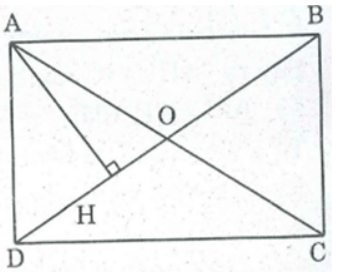
Ta có:
DB = HD + HB = 2 + 6 = 8 (cm)
AC = DB (tính chất hình chữ nhật)
OA = OB = OC = OD = 1/2 BD = 4 (cm)
OD = OH + HD
⇒ OH = OD – HD = 4 – 2 = 2 (cm)
Suy ra: ΔADO cân tại A
⇒AD = AO = 4 (cm)
Trong tam giác vuông ABD có ∠(BAD) = 90o
BD2 = AB2 + AD2 (định lý Pi-ta-go) ⇒ AB2 = BD2 - AD2
AB = √(BD2- AD2 ) = √(82-42 ) ≈ 7 (cm).
Bài 117 trang 94 SBT Toán 8 Tập 1: Chứng minh rằng ba điểm C, B, D ở hình dưới thẳng hàng.
Lời giải:
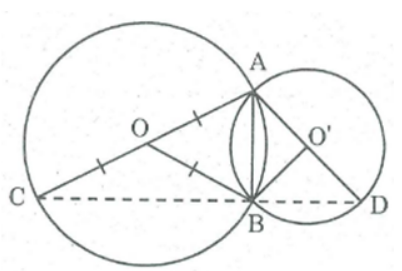
Nối AB, BO, BC, BO', BD.
* Trong ΔABC, ta có: OA = OC = R (bán kính đường tròn (O))
Nên BO là đường trung tuyến của ΔABC.
Mà BO = R (bán kính (O)) ⇒ BO = OA= OC = 1/2 AC
Suy ra tam giác ABC vuông tại B ⇒ ∠(ABC) = 90o
* Trong ΔABD , ta có: AO' = O'D = R' (bán kính đường tròn (O))
Nên BO' là đường trung tuyến của AABC.
Mà BO' = R' (bán kính (O')) ⇒ BO' = AO' = O'D = 1/2 AD
Suy ra tam giác ABC vuông tại B ⇒ ∠(ABD) = 90o
Ta có: ∠(ABC) + ∠(ABD) = ∠(CBD) = 90o + 90o = 180o.
Vậy C, B, D thẳng hàng.
Bài 118 trang 94 SBT Toán 8 Tập 1: Tứ giác ABCD có AB ⊥ CD. Gọi E, F, G, H theo thứ tự là trung điểm của BC, BD, AD, AC. Chứng minh rằng EG = FH.
Lời giải:
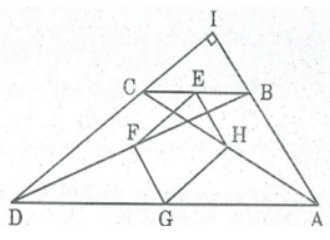
* Trong ΔBCD, ta có:
E là trung điểm của BG (gt)
F là trung điểm của BD (gt)
Suy ra EF là đường trung bình của ΔBCD
⇒ EF // CD và EF = 1/2 CD (1)
* Trong ΔACD, ta có: H là trung điểm của AC (gt)
G là trung điểm của AD (gt)
Suy ra HG là đường trung bình của ΔACD
⇒ HG //AC và HG = 1/2 AC (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
* Mặt khác: EF // CD (chứng minh trên)
AB ⊥ CD (gt)
Suy ra EF ⊥ AB
Trong ΔABC ta có HE là đường trung bình ⇒ HE // AB
Suy ra: HE ⊥ EF hay (FEH) = 90o
Vậy hình bình hành EFGH là hình chữ nhật.
Bài 119 trang 94 SBT Toán 8 Tập 1: Cho tam giác ABC, đường cao AH. Gọi D, E, M theo thứ tự là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác DEMH là hình thang cân.
Lời giải:
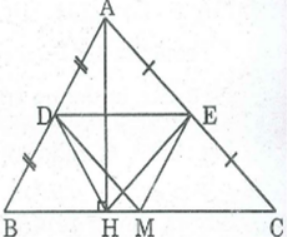
* Vì D trung điểm của AB (gt) và E trung điểm của AC (gt) nên DE là đường trung bình của tam giác ABC
⇒ DE // BC hay DE // HM
Suy ra tứ giác DEMH là hình thang
* Mà M trung điểm BC (gt) nên DM là đường trung bình của ∆BAC
⇒ DM = 1/2 AC (tính chất đường trung bình của tam giác) (1)
* Trong tam giác vuông AHC có ∠(AHC) = 90o. HE là trung tuyến thuộc cạnh huyền AC.
⇒ HE = 1/2 AC (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: DM = HE
Vậy hình thang DEMH là hình thang cân (vì có 2 đường chéo DM và EH bằng nhau).

