(SGK + SBT) Giải Toán 8 trang 95 Kết nối tri thức, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 95 Kết nối tri thức, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 95.
(SGK + SBT) Giải Toán 8 trang 95 Kết nối tri thức, Cánh diều
- Toán lớp 8 trang 95 Tập 1 (sách mới):
- Toán lớp 8 trang 95 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 95 (sách cũ)
Bài 120 trang 95 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A, điểm D thuộc cạnh AC. Gọi E, F, G theo thứ tự là trung điểm của BD, BC, DC. Chứng minh rằng tứ giác AEFG là hình thang cân.
Lời giải:
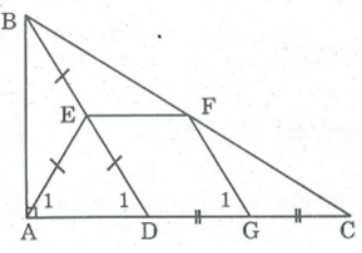
* Trong ΔBDC, ta có:
E là trung điểm của BD (gt)
F là trung điểm của BC (gt)
Suy ra EF là đường trung bình của tam giác BOD
⇒ EF // DC hay EF // AG
Suy ra tứ giác AEFG là hình thang
G là trung điểm của DC (gt)
Nên FG là đường trung bình của tam giác BCD
⇒ FG // BD ⇒ ∠Go= ∠Do(đồng vị) (1)
* Trong tam giác ABD vuông tại A có AE là trung tuyến thuộc cạnh huyền BD
⇒ AE = ED = 1/2 BD (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠Ao= ∠Go
Vậy hình thang AEFG là hình thang cân.
Bài 121 trang 95 SBT Toán 8 Tập 1: Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K theo thứ tự là chân đường vuông góc kẻ từ B, C đến đường thẳng DE. Chứng minh rằng EH = DK.
Lời giải:
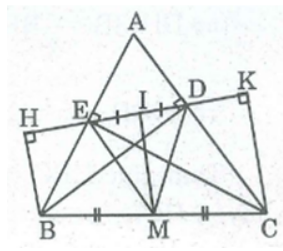
* Ta có: BH ⊥ DE (gt)
CK ⊥ DE (gt)
⇒ BH // CK hay tứ giác BHKC là hình thang
Gọi M là trung điểm của BC, I là trung điểm của DE
* Trong tam giác BDG vuông tại D có DM là trung tuyến thuộc cạnh huyền BC.
⇒ DM = 1/2 BC (tính chất tam giác vuông)
* Trong tam giác BEC vuông tại E có EM là đường trung tuyến thuộc cạnh huyền BC.
⇒ EM = 1/2 BC (tính chất tam giác vuông)
Suy ra: DM = EM nên ΔMDE cân tại M
MI là đường trung tuyến nên MI là đường cao ⇒ MI ⊥ DE
Suy ra: MI // BH // CK
BM = MC
Suy ra: HI = IK (tính chất đường trung bình hình thang)
⇒ HE + EI = ID + DK
Mà EI = ID nên EH = DK
Bài 122 trang 95 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC.
a. Chứng minh rằng AH = DE
b. Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh rằng DI // EK
Lời giải:
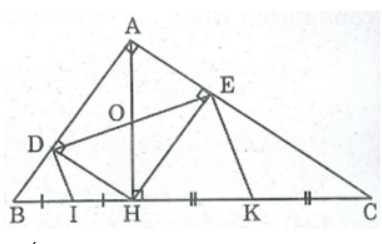
a. Xét tứ giác ADHE, ta có:
∠A = 90o (gt)
∠(ADH) = 90o (vì HD ⊥ AB)
∠(AEH) = 90o (Vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông)
Vậy AH = DE (tính chất hình chữ nhật)
b. Tam giác BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH
⇒ DI = IB = 1/2 BH (tính chất tam giác vuông)
⇒ ΔIDB cân tại 1 ⇒ ∠(DIB) = (180o - ∠B )/2 (1)
Tam giác HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.
⇒ EK = KH = 1/2 HC (tính chất tam giác vuông) .
⇒ ΔKHE cân tại K ⇒ ∠(EKH) = (180o - ∠(KHE) )/2 (2)
Tứ giác ADHE là hình chữ nhật nên:
HE // AD hay HE // AB ⇒ ∠B = ∠(KHE) (đồng vị)
Từ (1), (2) và (3) suy ra: ∠(DIB) = ∠(EKH)
Vậy DI // DK (vì có cặp góc đồng vị bằng nhau).
Bài 123 trang 95 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM.
a. Chứng minh rằng ∠(HAB) = ∠(MAC)
b. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AG. Chứng minh rằng AM vuông góc với DE.
Lời giải:
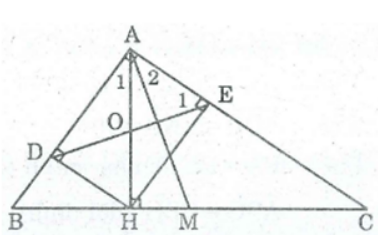
a. Ta có: AH ⊥ BC (gt) ⇒ ∠(HAB) + ∠B = 90o
Lại có: ∠B + ∠C = 90o (vì ΔABC có ∠A = 90o)
Suy ra ∠(HAB) = ∠C (1)
ΔABC vuông tại A có AM là trung tuyến thuộc cạnh huyền BC
⇒ AM = MC = 1/2 BC (tính chất tam giác vuông)
⇒ ΔMAC cân tại M ⇒ ∠(MAC) = ∠C (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠(HAB) = ∠(MAC)
b. Xét tứ giác ADHE, ta có:
∠A = 90o (gt)
∠(ADH) = 90o (vì HD ⊥ AB)
∠(AEH) = 90o (vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông).
⇒ ΔADH = ΔEHD (c.c.c) ⇒ ∠A1 = ∠(HED)
(HED) + ∠E1= ∠(HEA) = 90o
Suy ra: ∠E1+ ∠A1= 90o
∠A1= ∠A2(chứng minh trên) ⇒ ∠E1+ ∠A2= 90o
Gọi I là giao điểm của AM và DE.
Trong ΔAJE ta có: ∠(AIE) = 180o – (∠E1+ ∠A1) = 180o - 90o = 90o
Vậy AM ⊥ DE.

