Giải Toán 8 trang 10 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

---

Haylamdo giới thiệu lời giải bài tập Toán 8 trang 10 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 10.

Giải Toán 8 trang 10 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

• Giải Toán 8 trang 10 Chân trời sáng tạo

  Xem lời giải

• Giải Toán 8 trang 10 Kết nối tri thức

  Xem lời giải

• Giải Toán 8 trang 10 Cánh diều

  Xem lời giải

---

---

---

Lưu trữ: Giải Toán 8 trang 10 Bài 8 (sách cũ)

Bài 27 trang 10 sách bài tập Toán 8 Tập 2: Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba.

a. (√3 - x√5 )(2x√2 + 1) = 0

b. (2x - √7 )(x√10 + 3) = 0

c. (2 – 3x√5 )(2,5x + √2 ) = 0

d. (√13 + 5x)(3,4 – 4x√1,7 ) = 0

Lời giải:

a. (√3 - x√5 )(2x√2 + 1) = 0 ⇔ √3 - x√5 = 0 hoặc 2x√2 + 1 = 0

√3 - x√5 = 0 ⇔ x = √3/√5 ≈ 0,775

2x√2 + 1 = 0 ⇔ x = - 1/2√2 ≈ - 0,354

Phương trình có nghiệm x = 0,775 hoặc x = - 0,354

b. (2x - √7 )(x√10 + 3) = 0 ⇔ 2x - √7 = 0 hoặc x√10 + 3 = 0

2x - √7 = 0 ⇔ x = √7/2 ≈ 1,323

x√10 + 3 = 0 ⇔ x = - 3/√10 ≈ - 0,949

Phương trình có nghiệm x = 1,323 hoặc x = - 0,949

c. (2 – 3x√5 )(2,5x + √2 ) = 0 ⇔ 2 – 3x√5 = 0 hoặc 2,5x + √2 = 0

2 – 3x√5 = 0 ⇔ x = 2/3√5 ≈ 0,298

2,5x + √2 = 0 ⇔ x = - √2/ (2,5) ≈ - 0,566

Phương trình có nghiệm x = 0,298 hoặc x = - 0,566

d. (√13 + 5x)(3,4 – 4x√1,7 ) = 0

⇔13 + 5x = 0 hoặc 3,4 – 4x√1,7 = 0

√13 + 5x = 0 ⇔ x = - √13/ 5 ≈ - 0,721

3,4 – 4x√1,7 = 0 ⇔ x = 3,4/(4√1,7 ) ≈ 0,652

Phương trình có nghiệm x = - 0,721 hoặc x = 0,652

Bài 28 trang 10 sách bài tập Toán 8 Tập 2: Giải các phương trình sau:

a. (x – 1)(5x + 3) = (3x – 8)(x – 1)

b. 3x(25x + 15) – 35(5x + 3) = 0

c. (2 – 3x)(x + 11) = (3x – 2)(2 – 5x)

d. (2x² + 1)(4x – 3) = (2x² + 1)(x – 12)

e. (2x – 1)² + (2 – x)(2x – 1) = 0

f. (x + 2)(3 – 4x) = x² + 4x + 4

Lời giải:

a. (x – 1)(5x + 3) = (3x – 8)(x – 1)

⇔ (x – 1)(5x + 3) – (3x – 8)(x – 1) = 0

⇔ (x – 1)[(5x + 3) – (3x – 8)] = 0

⇔ (x – 1)(5x + 3 – 3x + 8) = 0

⇔ (x – 1)(2x + 11) = 0 ⇔ x – 1 = 0 hoặc 2x + 11 = 0

x – 1 = 0 ⇔ x = 1

2x + 11 = 0 ⇔ x = -5,5

Vậy phương trình có nghiệm x = 1 hoặc x = -5,5

b. 3x(25x + 15) – 35(5x + 3) = 0

⇔ 15x(5x + 3) – 35(5x + 3) = 0

⇔ (15x – 35)(5x + 3) = 0 ⇔ 15x – 35 = 0 hoặc 5x + 3 = 0

15x – 35 = 0 ⇔ x = 35/15 = 7/3

5x + 3 = 0 ⇔ x = - 3/5

Vậy phương trình có nghiệm x = 7/3 hoặc x = -3/5

c. (2 – 3x)(x + 11) = (3x – 2)(2 – 5x)

⇔ (2 – 3x)(x + 11) – (3x – 2)(2 – 5x) = 0

⇔ (2 – 3x)(x + 11) + (2 – 3x)(2 – 5x) = 0

⇔ (2 – 3x)[(x + 11) + (2 – 5x)] = 0

⇔ (2 – 3x)(x + 11 + 2 – 5x) = 0

⇔ (2 – 3x)(13 – 4x) = 0 ⇔ 2 – 3x = 0 hoặc 13 – 4x = 0

2 – 3x = 0 ⇔ x = 2/3

13 – 4x = 0 ⇔ x = 13/4

Vậy phương trình có nghiệm x = 2/3 hoặc x = 13/4

d. (2x² + 1)(4x – 3) = (2x² + 1)(x – 12)

⇔ (2x² + 1)(4x – 3) – (2x² + 1)(x – 12) = 0

⇔ (2x² + 1)[(4x – 3) – (x – 12)] = 0

⇔ (2x² + 1)(4x – 3 – x + 12) = 0

⇔ (2x² + 1)(3x + 9) = 0 ⇔ 2x² + 1 = 0 hoặc 3x + 9 = 0

2x² + 1 = 0: vô nghiệm (vì 2x² ≥ 0 nên 2x² + 1 > 0)

3x + 9 = 0 ⇔ x = - 3

Vậy phương trình có nghiệm x = -3

e. (2x – 1)² + (2 – x)(2x – 1) = 0

⇔ (2x – 1)(2x – 1) + (2 – x)(2x – 1) = 0

⇔ (2x – 1)[(2x – 1) + (2 – x)] = 0

⇔ (2x – 1)(2x – 1 + 2 – x) = 0

⇔ (2x – 1)(x + 1) = 0 ⇔ 2x – 1 = 0 hoặc x + 1 = 0

2x – 1 = 0 ⇔ x = 0,5

x + 1 = 0 ⇔ x = - 1

Vậy phương trình có nghiệm x = 0,5 hoặc x = - 1

f. (x + 2)(3 – 4x) = x² + 4x + 4

⇔ (x + 2)(3 – 4x) – (x + 2)² = 0

⇔ (x + 2)(3 – 4x) – (x + 2)(x + 2) = 0

⇔ (x + 2)[(3 – 4x) – (x + 2)] = 0

⇔ (x + 2)(3 – 4x – x – 2) = 0

⇔ (x + 2)(1 – 5x) = 0 ⇔ x + 2 = 0 hoặc 1 – 5x = 0

x + 2 = 0 ⇔ x = - 2

1 – 5x = 0 ⇔ x = 0,2

Vậy phương trình có nghiệm x = - 2 hoặc x = 0,2

Bài 29 trang 10 sách bài tập Toán 8 Tập 2: Giải các phương trình sau:

a. (x – 1)(x² + 5x – 2) – (x³ – 1) = 0

b. x² + 9x + 2)(11x – 7) = 4

c. x³ + 1 = x(x + 1)

d. x³ + x² + x + 1 = 0

Lời giải:

a. (x – 1)(x² + 5x – 2) – (x³ – 1) = 0

⇔ (x – 1)(x² + 5x – 2) – (x – 1)(x² + x + 1) = 0

⇔ (x – 1)[(x² + 5x – 2) – (x² + x + 1)] = 0

⇔ (x – 1)(x² + 5x – 2 – x² – x – 1) = 0

⇔ (x – 1)(4x – 3) = 0 ⇔ x – 1 = 0 hoặc 4x – 3 = 0

x – 1 = 0 ⇔ x = 1

4x – 3 = 0 ⇔ x = 0,75

Vậy phương trình có nghiệm x = 1 hoặc x = 0,75

b. x² + 9x + 2)(11x – 7) = 4

⇔ x² – 4 + (x + 2)(11x – 7) = 0

⇔ (x + 2)(x – 2) + (x + 2)(11x – 7) = 0

⇔ (x + 2)[(x – 2) + (11x – 7)] = 0

⇔ (x + 2)(x – 2 + 11x – 7) = 0

⇔ (x + 2)(12x – 9) = 0 ⇔ x + 2 = 0 hoặc 12x – 9 = 0

x + 2 = 0 ⇔ x = - 2

12x – 9 = 0 ⇔ x = 0,75

Vậy phương trình có nghiệm x = - 2 hoặc x = 0,75

c. x³ + 1 = x(x + 1)

⇔ (x + 1)(x² – x + 1) = x(x + 1)

⇔ (x + 1)(x² – x + 1) – x(x + 1) = 0

⇔ (x + 1)(x² – x + 1 – x) = 0

⇔ (x + 1)(x² – 2x + 1) = 0

⇔ (x + 1)(x – 1)² = 0 ⇔ x + 1 = 0 hoặc (x – 1)² = 0

x + 1 = 0 ⇔ x = - 1

(x – 1)² = 0 ⇔ x – 1 = 0 ⇔ x = 1

Vậy phương trình có nghiệm x = -1 hoặc x = 1

d. x³ + x² + x + 1 = 0

⇔ x²(x + 1) + (x + 1) = 0

⇔ (x² + 1)(x + 1) = 0 ⇔ x² + 1 = 0 hoặc x + 1 = 0

x² + 1 = 0: vô nghiệm (vì x² ≥ 0 nên x² + 1 > 0)

x + 1 = 0 ⇔ x = - 1

Vậy phương trình có nghiệm x = - 1

Bài 30 trang 10 sách bài tập Toán 8 Tập 2: Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích:

a. x² – 3x + 2 = 0

b. – x² + 5x – 6 = 0

c. 4x² – 12x + 5 = 0

d. 2x² + 5x + 3 = 0

Lời giải:

a. x² – 3x + 2 = 0 ⇔ x² – x – 2x + 2 = 0

⇔ x(x – 1) – 2(x – 1) = 0 ⇔ (x – 2)(x – 1) = 0

⇔ x – 2 = 0 hoặc x – 1 = 0

x – 2 = 0 ⇔ x = 2

x – 1 = 0 ⇔ x = 1

Vậy phương trình có nghiệm x= 2 hoặc x = 1

b. – x² + 5x – 6 = 0 ⇔ - x² + 2x + 3x – 6 = 0

⇔ - x(x – 2) + 3(x – 2) = 0 ⇔ (x – 2)(3 – x) = 0

⇔ x – 2 = 0 hoặc 3 – x = 0

x – 2 = 0 ⇔ x = 2

3 – x = 0 ⇔ x = 3

Vậy phương trình có nghiệm x = 2 hoặc x = 3.

c. 4x² – 12x + 5 = 0 ⇔ 4x² – 2x – 10x + 5 = 0

⇔ 2x(2x – 1) – 5(2x – 1) = 0 ⇔ (2x – 1)(2x – 5) = 0

⇔ 2x – 1 = 0 hoặc 2x – 5 = 0

2x – 1 = 0 ⇔ x = 0,5

2x – 5 = 0 ⇔ x = 2,5

Vậy phương trình có nghiệm x = 0,5 hoặc x = 2,5

d. 2x² + 5x + 3 = 0 ⇔ 2x² + 2x + 3x + 3 = 0

⇔ 2x(x + 1) + 3(x + 1) = 0 ⇔ (2x + 3)(x + 1) = 0

⇔ 2x + 3 = 0 hoặc x + 1 = 0

2x + 3 = 0 ⇔ x = -1,5

x + 1 = 0 ⇔ x = -1

Vậy phương trình có nghiệm x = -1,5 hoặc x = -1

Bài 31 trang 10 sách bài tập Toán 8 Tập 2: Giải các phương trình bằng cách đưa về dạng phương trình tích:

a. (x - √2 ) + 3(x² – 2) = 0

b. x² – 5 = (2x - √5 )(x + √5 )

Lời giải:

a. (x - √2 ) + 3(x² – 2) = 0 ⇔ (x - √2 )+ 3(x + √2 )(x - √2 ) = 0

⇔ (x - √2 )[1 + 3(x + √2 )] = 0 ⇔ (x - √2 )(1 + 3x + 3√2 ) = 0

⇔ x - √2 = 0 hoặc 1 + 3x + 3√2 = 0

x - √2 = 0 ⇔ x = √2

1 + 3x + 3√2 = 0

⇔ x =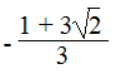

Vậy phương trình có nghiệm x = 2 hoặc x =

b. x² – 5 = (2x - √5 )(x + √5 )

⇔ (x + √5 )(x - √5 ) = (2x - √5 )(x + √5 )

⇔ (x + √5 )(x - √5 ) – (2x - √5 )(x + √5 ) = 0

⇔ (x + √5 )[(x - √5 ) – (2x - √5 )] = 0

⇔ (x + √5 )(- x) = 0 ⇔ x + 5 = 0 hoặc – x = 0

x + √5 = 0 ⇔ x = - √5

x = 0 ⇔ x = 0

Vậy phương trình có nghiệm x = - √5 hoặc x = 0.

Bài 32 trang 10 sách bài tập Toán 8 Tập 2: Cho phương trình (3x + 2k – 5)(x – 3k + 1) = 0, trong đó k là một số.

a. Tìm các giá trị của k sao cho mộ trong các nghiệm của phương trình là x = 1.

b. Với mỗi giá trị của k tìm được trong câu a, hãy giải phương trình đã cho.

Lời giải:

a. Thay x = 1 vào phương trình (3x + 2k – 5)(x – 3k + 1) = 0, ta có:

(3.1 + 2k – 5)(1 – 3k + 1) = 0

⇔ (2k – 2)(2 – 3k) = 0 ⇔ 2k – 2 = 0 hoặc 2 – 3k = 0

2k – 2 = 0 ⇔ k = 1

2 – 3k = 0 ⇔ k = 2/3

Vậy với k = 1 hoặc k = 2/3 thì phương trình đã cho có nghiệm x = 1

b. Với k = 1, ta có phương trình:

(3x – 3)(x – 2) = 0 ⇔ 3x – 3 = 0 hoặc x – 2 = 0

3x – 3 = 0 ⇔ x = 1

x – 2 = 0 ⇔ x = 2

Vậy phương trình có nghiệm x = 1 hoặc x = 2

Với k = 2/3 , ta có phương trình:

(3x - 11/3 )(x – 1) = 0 ⇔ 3x - 11/3 = 0 hoặc x – 1 = 0

3x - 11/3 = 0 ⇔ x = 11/9

x – 1 = 0 ⇔ x = 1

Vậy phương trình có nghiệm x = 11/9 hoặc x = 1.