(SGK + SBT) Giải Toán 8 trang 16 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

---

Haylamdo giới thiệu lời giải bài tập Toán 8 trang 16 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 16.

(SGK + SBT) Giải Toán 8 trang 16 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

- Toán lớp 8 trang 16 Tập 1 (sách mới):

• Giải Toán 8 trang 16 Chân trời sáng tạo

  Xem lời giải

• Giải Toán 8 trang 16 Cánh diều

  Xem lời giải

• Giải Toán 8 trang 16 Kết nối tri thức

  Xem lời giải

- Toán lớp 8 trang 16 Tập 2 (sách mới):

---

---

---

Lưu trữ: Giải SBT Toán 8 trang 16 (sách cũ)

Bài 62 trang 16 sách bài tập Toán 8 Tập 2: Cho hai biểu thức A = 5/(2m + 1) và B = 4/(2m - 1) . Hãy tìm các giá trị của m để hai biểu thức ấy có giá trị thỏa mãn hệ thức:

a. 2A + 3B = 0

b. A.B = A + B

Lời giải:

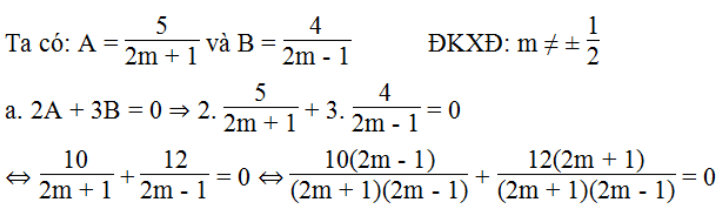
⇔ 10(2m – 1) + 12(2m + 1) = 0

⇔ 20m – 10 + 24m + 12 = 0

⇔ 44m + 2 = 0

⇔ m = - 1/22 (thỏa)

Vậy m = - 1/22 thì 2A + 3B = 0.

b. A.B = A + B

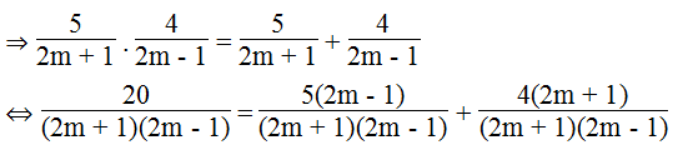
⇔ 20 = 5(2m – 1) + 4(2m + 1)

⇔ 20 = 10m – 5 + 8m + 4

⇔ 18m = 21

⇔ m = 7/6 (thỏa)

Vậy m = 7/6 thì A.B = A + B

Bài 63 trang 16 sách bài tập Toán 8 Tập 2: Tính gần đúng nghiệm của các phương trình sau, làm tròn đến chữ số thập phân thứ hai.

a. (x√13 + √5 )(√7 – x√3 ) = 0

b. (x√2,7 – 1,54)(√1,02 + x√3,1) = 0

Lời giải:

a. (x√13 + √5 )(√7 – x√3 ) = 0

⇔ x√13 + √5 = 0 hoặc √7 - x√3 = 0

x√13 + √5 = 0 ⇔ x = - √5 / √13 ≈ -0,62

√7 - x√3 = 0 ⇔ x = √7 / √3 ≈ 1,53

Vậy phương trình có nghiệm x = -0,62 hoặc x = 1,53

b. (x√2,7 – 1,54)(√1,02 + x√3,1) = 0

⇔ x√2,7 – 1,54 = 0 hoặc √1,02 + x√3,1 = 0

x√2,7 – 1,54 = 0 ⇔ x = 1,54/√2,7 ≈ 0,94

√1,02 + x√3,1 = 0 ⇔ x = - √1,02/√3,1 ≈ - 0,57

Vậy phương trình có nghiệm x = 0,94 hoặc x = - 0,57.

Bài 64 trang 16 sách bài tập Toán 8 Tập 2: Giải các phương trình sau:

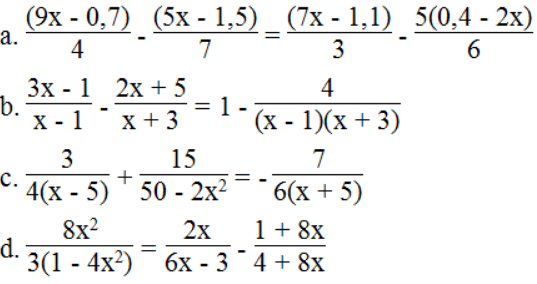
Lời giải:

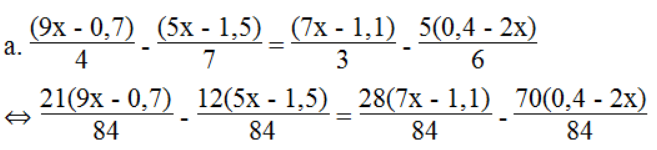
⇔ 21(9x – 0,7) – 12(5x – 1,5) = 28(7x – 1,1) – 70(0,4 – 2x)

⇔ 189x – 14,7 – 60x + 18 = 196x – 30,8 – 28 + 140x

⇔ 189x – 60x – 196x – 140x = - 30,8 – 28 + 14,7 – 18

⇔ - 207x = - 62,1 ⇔ x = 0,3

Vậy phương trình có nghiệm x = 0,3

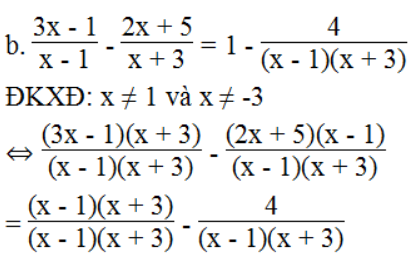
⇔ (3x – 1)(x + 3) – (2x + 5)(x – 1) = (x – 1)(x + 3) – 4

⇔ 3x² + 9x – x – 3 – 2x² + 2x – 5x + 5 = x² + 3x – x – 3 – 4

⇔ 3x² – 2x² – x² + 9x – x + 2x – 5x – 3x + x = -3 – 4 + 3 – 5

⇔ 3x = - 9 ⇔ x = - 3 (loại)

Vậy phương trình vô nghiệm.

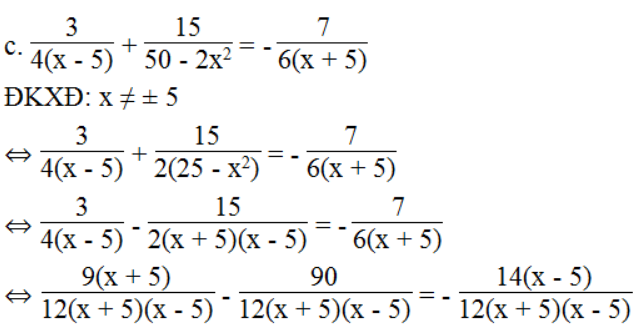
⇔ 9(x + 5) – 90 = - 14(x – 5) ⇔ 9x + 45 – 90 = - 14x + 70

⇔ 9x + 14x = 70 – 45 + 90 ⇔ 23x = 115 ⇔ x = 5 (loại)

Vậy phương trình vô nghiệm.

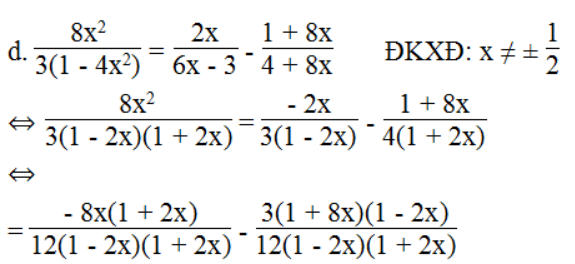
⇔ 32x² = - 8x(1 + 2x) – 3(1 + 8x)(1 – 2x)

⇔ 32x² = - 8x – 16x² – 3 – 18x + 48x²

⇔ 32x² + 16x² – 48x² + 18x + 8x = - 3

⇔ 26x = - 3 ⇔ x = - 3/26 (thỏa)

Vậy phương trình có nghiệm x = - 3/26 .

Bài 65 trang 16 sách bài tập Toán 8 Tập 2: Cho phương trình (ẩn x): 4x² – 25 + k² + 4kx = 0

a. Giải phương trình với k = 0

b. Giải phương trình với k = - 3

c. Tìm các giá trị của k sao cho phương trình nhận x = - 2 làm nghiệm

Lời giải:

a. Khi k = 0 ta có phương trình: 4x² – 25 = 0

⇔ (2x + 5)(2x – 5) = 0

⇔ 2x + 5 = 0 hoặc 2x – 5 = 0

2x + 5 = 0 ⇔ x = - 5/2

2x – 5 = 0 ⇔ x = 5/2

Vậy phương trình có nghiệm x = - 5/2 hoặc x = 5/2

b. Khi k = - 3 ta có phương trình: 4x² – 25 + (-3)2 + 4(-3)x = 0

⇔ 4x² – 25 + 9 – 12x = 0

⇔ 4x² – 12x – 16 = 0

⇔ x² – 3x – 4 = 0

⇔ x² – 4x + x – 4 = 0

⇔ x(x – 4) + (x – 4) = 0

⇔ (x + 1)(x – 4) = 0

⇔ x + 1 = 0 hoặc x – 4 = 0

x + 1 = 0 ⇔ x = -1

x – 4 = 0 ⇔ x = 4

Vậy phương trình có nghiệm x = -1 hoặc x = 4.

c. Phương trình nhận x = -2 làm nghiệm nên ta có:

4(-2)² – 25 + k² + 4k(-2) = 0

⇔ 16 – 25 + k² – 8k = 0

⇔ k² – 8k – 9 = 0

⇔ k² – 9k + k – 9 = 0

⇔ k(k – 9) + (k – 9) = 0

⇔ (k + 1)(k – 9) = 0

⇔ k + 1 = 0 hoặc k – 9 = 0

k + 1 = 0 ⇔ k = -1

k – 9 = 0 ⇔ k = 9

Vậy k = -1 hoặc k = 9 thì phương trình nhận x = -2 làm nghiệm.