Bài I.1, I.2, I.3, I.4, I.5 trang 123 SBT Toán 9 Tập 1

---

Bài I.1, I.2, I.3, I.4, I.5 trang 123 SBT Toán 9 Tập 1

Bài 1 trang 123 Sách bài tập Toán 9 Tập 1: Tam giác ABC có A ̂ = 105^o, B ̂ = 45^o, BC = 4cm. Tính độ dài các cạnh AB, AC.

Lời giải:

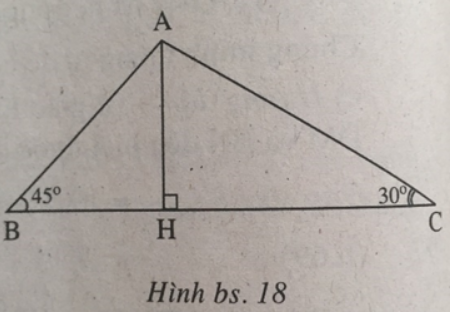
Vẽ đường cao AH. Đặt BH = x, CH = y thì do H nằm giữa B và C (hai góc ∠B, ∠C là góc nhọn) suy ra x + y = 4 (xem h.bs.18).

Ta có BH = AH = HC.tg30^o nên x – y.tg30^o = y/√3.

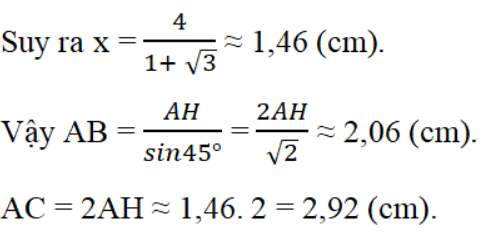
AC = 2AH ≈ 1,46. 2 = 2,92 (cm).

Bài 2 trang 123 Sách bài tập Toán 9 Tập 1: Cho hình vuông ABCD có cạnh bằng 2a. Gọi M, N lần lượt là trung điểm của BC, CD. Tính cos(MAN).

Lời giải:

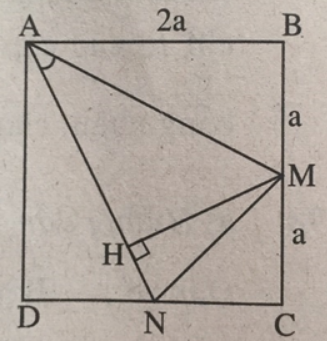
Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠(NAM) = HM/AM và diện tích tam giác AMN là S_AMN = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 AN².sin(NAM) = 1/2(AD² + DN²). sin(NAM) = (5a²)/2 sin(NAM).

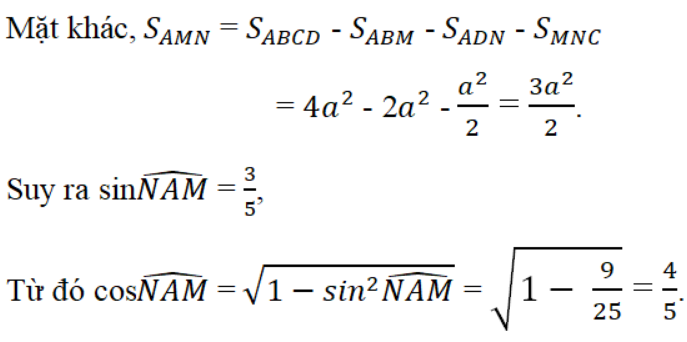
Bài 3 trang 123 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC cân tại A, đường cao BH. Hãy tính góc A và các cạnh AB, BC, nếu biết BH = h, ∠C = α.

Lời giải:

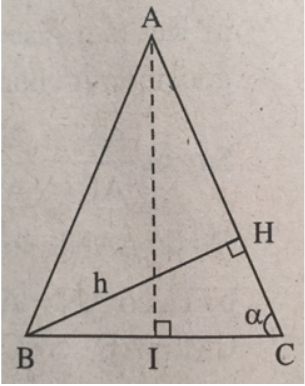
∠A = 180² - 2α. Tam giác vuông HBC có BC = h/sinα. Kẻ đường cao AI của tam giác ABC thì được

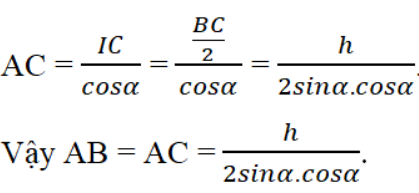
Bài 4 trang 123 Sách bài tập Toán 9 Tập 1: Hình bình hành ABCD có ∠A = 120^o, AB = a, BC = b. Các đường phân giác của bốn góc A, B, C, D cắt nhau tạo thành tứ giác MNPQ. Tính diện tích tứ giác MNPQ.

Lời giải:

Đường phân giác của góc A cắt đường phân giác của góc D tại M thì tam giác ADM có hai góc bằng 60o và 30o nên các đường phân giác đó vuông góc với nhau. Lập luận đó chứng tỏ hình MNPQ có 4 góc vuông nên MNPQ là hình chữ nhật.

Trong tam giác vuông ADM có

DM = AD.sin(DAM) ̂ = b.sin60^o = (b√3)/2.

Trong tam giác vuông DCN (N là giao điểm của đường phân giác góc D và đường phân giác góc C) có DN = DCsin(DCN) = a.sin60^o = (a√3)/2.

Vậy MN = DN – DM = (a – b).√3/2.

Trong tam giác vuông DCN có CN = CD.cos60^o = a/2. Trong tam giác vuông BCP (P là giao của đường phân giác góc C với đường phân giác góc B) có CP = CB.cos60^o = b/2. Vậy NP = CN – CP = (a-b)/2.

Suy ra diện tích hình chữ nhật MNPQ là:

MN x NP = (a-b)² √3/4.

Bài 5 trang 123 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại C có ∠B = 37². Gọi I là giao điểm của cạnh BC với đường trung trực của AB. Hãy tính AB, AC nếu biết BI = 20.

Lời giải:

Gọi H là trung điểm của AB thì trong tam giác vuông HBI, ta có HB = IB.cosB nên AB = 2HB = 2IB.cosB = 40cos37² ≈ 31,95.

Trong tam giác vuông ABC, ta có: AC = AB.sinB = 31,95.sin37² ≈ 19,23.