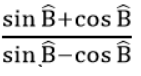Bài 88, 89, 90, 91, 92, 93 trang 121 SBT Toán 9 Tập 1

---

Bài 88, 89, 90, 91, 92, 93 trang 121 SBT Toán 9 Tập 1

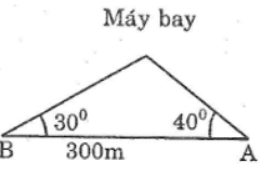
Bài 88 trang 121 Sách bài tập Toán 9 Tập 1: Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết khoảng cách giữa hai người này là 300m, góc “nâng” để nhìn thấy máy bay tại vị trí A là 40^o và tại vị trí B là 30^o (hình bên). Hãy tìm độ cao của máy bay.

Lời giải:

Gọi C là vị trí của máy bay.

Kẻ CH ⊥ AB

Trong tam giác vuông ACH, ta có:

AH = CH.cotg ∠A (1)

Trong tam giác vuông BCH, ta có:

BH = CH.cotg ∠B (2)

Từ (1) và (2) suy ra: (AH + BH) = CH.cotg ∠A + CH.cotg ∠B

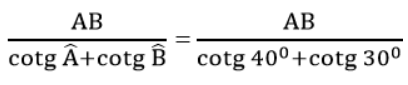
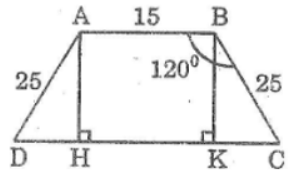
Suy ra: CH = ≈ 102,606 (cm)

Bài 89 trang 121 Sách bài tập Toán 9 Tập 1: Cho hình thang với đáy nhỏ là 15cm, hai cạnh bên bằng nhau và bằng 25cm, góc tù bằng 120o. Tính chu vi và diện tích hình thang đó.

Lời giải:

Giả sử hình thang ABCD có đáy nhỏ AB = 15cm, cạnh bên AD = BC = 25cm,

Mà ΔADH = ΔBCK (cạnh huyền, cạnh góc vuông)

Suy ra: DH = CK = 12,5 (cm)

Chu vi hình thang ABCD là:

AB + BC + CD + DA = AB + BC + (CK + KH + HD) + DA

= 15 + 25 + (12,5 + 15 + 12,5) + 25 = 105 (cm)

Chu vi hình thang ABCD là:

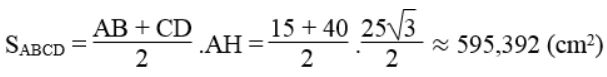
Bài 90 trang 121 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm.

a. Tính BC, góc B , góc C

b. Phân giác của góc A cắt BC ở D. Tính BD, CD

c. Từ D kẻ DE và DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình gì? Tính chu vi và diện tích tứ giác AEDF

Lời giải:

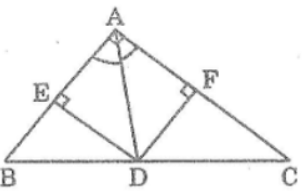
a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC ta có:

BC² = AB² + AC² = 6² + 8² = 36 + 64 = 100 (cm)

Suy ra: BC = √100 = 10 (cm)

Ta có: sinC = AB/BC = 6/10 = 0,6

Nên tứ giác AFDE là hình vuông

* Vì DE ⊥ AB, AC ⊥ AB nên DE // AC

Theo định lí Ta-lét ta có: CD/BC = AE/AB

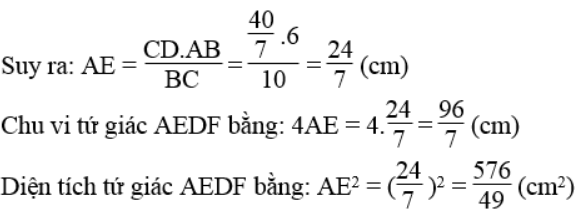
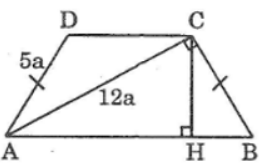
Bài 91 trang 121 Sách bài tập Toán 9 Tập 1: Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC

Biết AD = 5a, AC = 12a

a. Tính sin

b. Tính chiều cao của hình thang ABCD

Lời giải:

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC ta có:

AB² = BC² + AC² = (5a)² + (12a)² = 169a²

Bài 92 trang 121 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC, AB = AC = 10cm, BC = 16cm. Trên đường cao AH lấy điểm I sao cho AI = (1/3).AH. Vẽ tia Cx song song với AH, Cx cắt tia BI tại D

a. Tính các góc của tam giác ABC

b. Tính diện tích tứ giác ABCD

Lời giải:

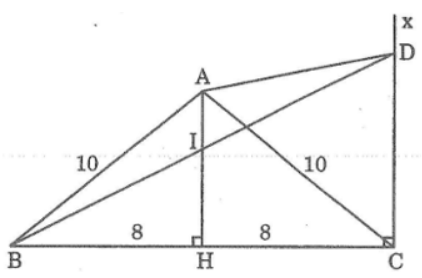
a. Ta có: AH ⊥ BC, suy ra: HB = HC = BC/2 = 8 (cm)

Trong tam giác vuông ABH, ta có:

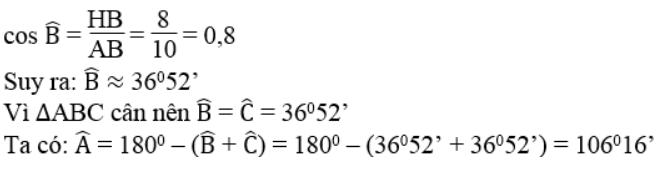
b. Áp dụng định lí Pi-ta-go vào tam giác vuông ABH ta có:

AB² = AH² + BH² ⇒ AH² = AB² – BH²= 10² – 8² = 36

Suy ra: AH = 6 (cm)

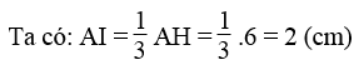
Suy ra: IH = AH – AI = 6 – 2 = 4 (cm)

Vì IH ⊥ BC và DC ⊥ BC nên IH // DC (1)

Mặt khác: BH = HC (gt) (2)

Từ (1) và (2) ta có IH là đường trung bình của tam giác BCD

Bài 93 trang 121 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC, biết AB = 21cm, AC = 28cm, BC = 35cm.

a. Chứng minh tam giác ABC vuông

b. Tính sin ∠B , sin ∠C

Lời giải:

a. Ta có: AB² = 21² = 441

AC² = 28² = 784

BC² = 35² = 1225

Vì AB² + AC² = 441 + 784 = 1225 = BC² nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)

b. Ta có: sin ∠B = AC/BC = 28/35 = 0,8

sin∠C = AB/BC = 21/35 = 0,6