Bài 94, 95, 96, 97, 98, 99 trang 122 SBT Toán 9 Tập 1

---

Bài 94, 95, 96, 97, 98, 99 trang 122 SBT Toán 9 Tập 1

Bài 94 trang 122 Sách bài tập Toán 9 Tập 1: Cho hình thang ABCD. Biết hai đáy AB = a và CD = 2a, cạnh bên AD = a, góc A = 90^o

a. Chứng minh tg ∠C = 1

b. Tính tỉ số diện tích tam giác BCD và diện tích hình thang ABCD

c. Tính tỉ số diện tích tam giác ABC và diện tích tam giác BCD

Lời giải:

a. Kẻ BH ⊥ CD

Ta có: AB // CD và góc A = 90^o

Suy ra:góc D = 90^o

Tứ giác ABHD có 3 góc vuông và AB = AD = a nên là hình vuông

Suy ra: DH = BH = AB = a

Ta có: CD = DH + HC

Suy ra: HC = CD – DH = 2a – a = a

Vậy tg ∠C = BH/CH = aa = 1

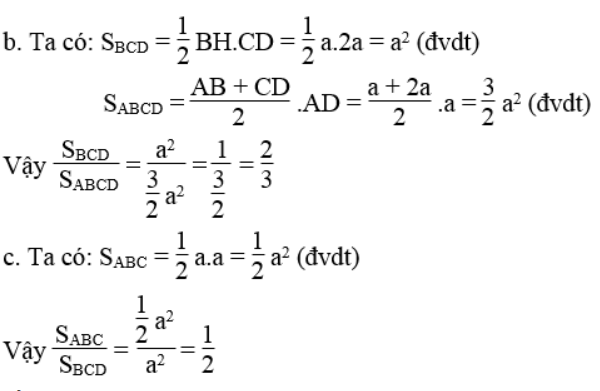
Bài 95 trang 122 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC có góc B bằng 120^o, BC = 12cm, AB = 6cm. Đường phân giác của góc B cắt cạnh AC tại D.

a. Tính độ dài đường phân giác BD

b. Gọi M là trung điểm của BC. Chứng minh AM ⊥ BD

Lời giải:

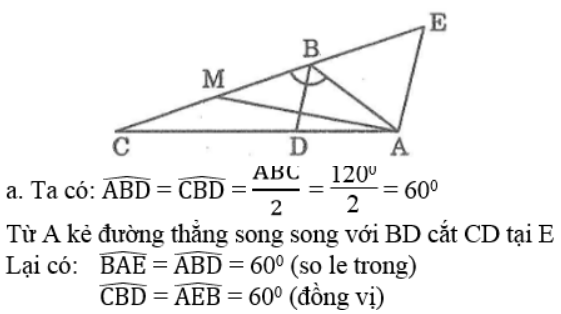
Suy ra tam giác ABE đều ⇒ AB = BE = EA = 6 (cm) (1)

Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)

Tam giác ACE có AE // BD nên suy ra:

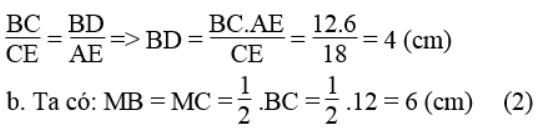
Từ (1) và (2) suy ra: BM = AB ⇒ ΔABM cân tại B

Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy BD ⊥ AM

Bài 96 trang 122 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC.

a. Tính độ dài đoạn thẳng DE

b. Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH

c. Tính diện tích tứ giác DENM

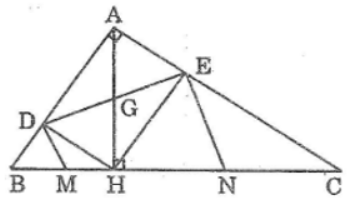
Lời giải:

Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật

Suy ra: AH = DE (tính chất hình chữ nhật)

Tam giác ABC vuông tại A và có AH là đường cao

Theo hệ thức giữa đường cao và hình chiếu ta có:

AH² = HB.HC = 4.9 = 36 ⇒ AH = 6 (cm)

Vậy DE = 6 (cm)

b. *Gọi G là giao điểm của AH và DE

Ta có: GA = GD = GH = GE (tính chất hình chữ nhật)

Suy ra tam giác GHD cân tại G

Suy ra tam giác NCE cân tại N ⇒ NC = NE (16)

Từ (13) và (16) suy ra: NC = NH hay N là trung điểm của CH.

c. Tam giác BDH vuông tại D có DM là đường trung tuyến nên:

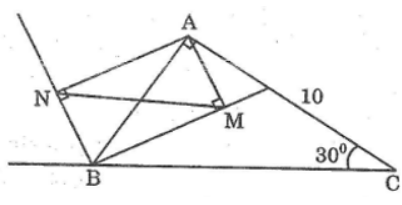
Bài 97 trang 122 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông ở A, góc C = 30^o, BC = 10cm

a. Tính AB, AC

b. Từ A kẻ AM, AN lần lượt vuông góc với các đường phân giác trong và ngoài của góc B. Chứng minh MN // BC và MN = AB

c. Chứng minh hai tam giác MAB và ABC đồng dạng. Tìm tỉ số đồng dạng

Lời giải:

a. Trong tam giác vuông ABC, ta có:

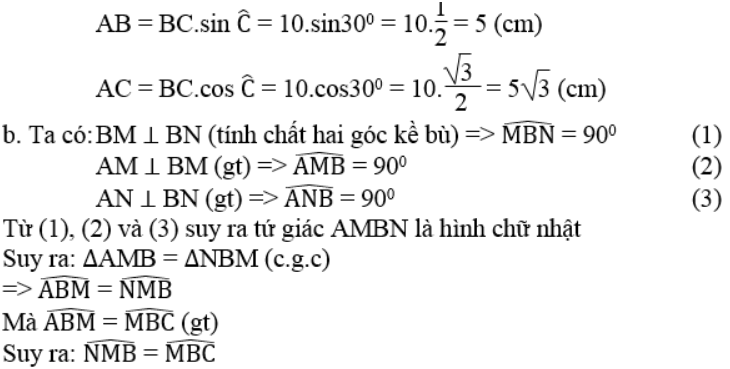
Suy ra: MN // BC (có cặp góc so le trong bằng nhau)

Vì AMBN là hình chữ nhật nên AB = MN

Bài 98 trang 122 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.

a. Chứng minh tam giác ABC vuông ở A. Tính các góc B , C và đường cao AH của tam giác

b. Tìm tập hợp các điểm M sao cho S_ABC = S_BMC

Lời giải:

a. Ta có: AB² = 6² = 36

AC² = 4,5² = 20,25

BC² = 7,5² = 56,25

Vì AB² + AC² = 36 + 20,25 = 56,25 = BC² nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)

Kẻ AH ⊥ BC

Ta có: AH.BC = AB.AC

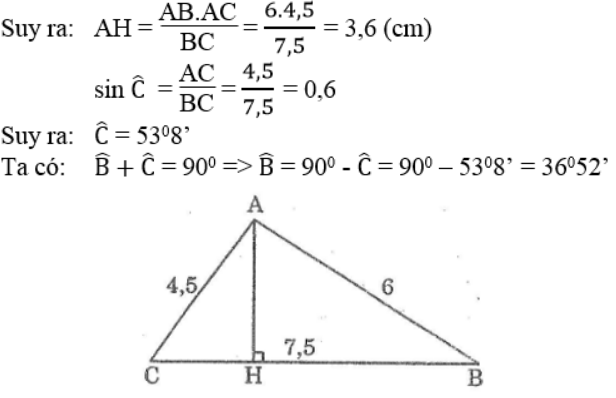
b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời S_ABC = S_MBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.

Bài 99 trang 122 Sách bài tập Toán 9 Tập 1: Gọi AM, BN, CL lần lượt là ba đường cao của tam giác ABC. Chứng minh:

a. Tam giác ANL và tam giác ABC đồng dạng

b. AN.BL.CM = AB.BC.CA.cos ∠A cos ∠B cos ∠C

Lời giải:

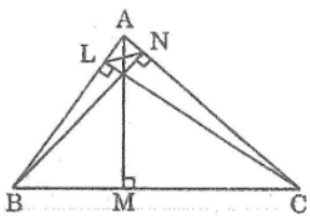
a. Xét hai tam giác BNA và CLA, ta có:

∠(BNA) = ∠(CLA)

∠ A chung

Suy ra ΔBNA đồng dạng ΔCLA (g.g)

Suy ra: AL/AN = AC/AB ⇒ AL/AC = AN/AB

Xét hai tam giác ABC và ANL, ta có:

AL/AC = AN/AB

∠ A chung

Suy ra ΔABC đồng dạng ΔANL (c.g.c)

b. ΔABN vuông tại N nên AN = AB.cos ∠ A (1)

ΔBCL vuông tại L nên BL = BC.cos∠ B (2)

ΔACM vuông tại M nên CM = AC.cos∠ C (3)

Từ (1), (2) và (3) suy ra: AN.BL.CM = AB.BC.CA. cos∠ A. cos∠ B. cos∠C