Bài 2.11, 2.12, 2.13, 2.14, 2.15, 2.16, 2.17, 2.18, 2.19, 2.20 trang 110 SBT Toán 9 Tập 1

---

Bài 2.11, 2.12, 2.13, 2.14, 2.15, 2.16, 2.17, 2.18, 2.19, 2.20 trang 110 SBT Toán 9 Tập 1

Bài 11 trang 110 Sách bài tập Toán 9 Tập 1: Tìm đẳng thức đúng

A. cotgα = 1 + tgα;     B. cotgα = 1 - tgα;

C. cotgα = 1. tgα;     D. cotgα = 1/tgα.

Lời giải:

Chọn đáp án D

Bài 12 trang 110 Sách bài tập Toán 9 Tập 1: Cho sinα = 1/2. Hãy tìm cosα, tgα, cotgα (0^o < α < 90^o).

Lời giải:

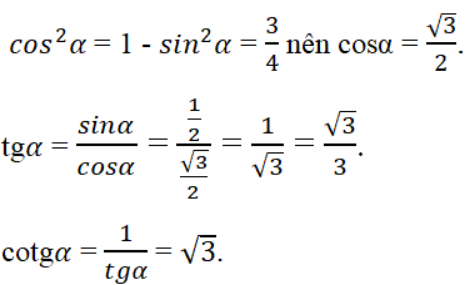
Bài 13 trang 110 Sách bài tập Toán 9 Tập 1: Cho cosα = 3/4. Hãy tìm sinα, tgα, cotgα (0^o < α < 90^o).

Lời giải:

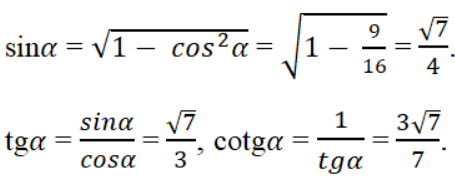
Bài 14 trang 110 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, có AB = 1/3BC. Hãy tính sinC, cosC, tgC, cotgC.

Lời giải:

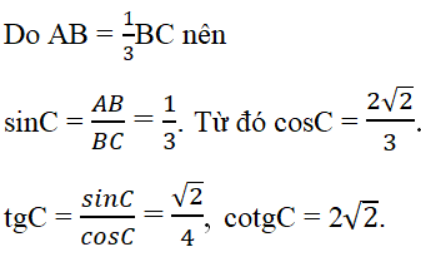
Bài 15 trang 110 Sách bài tập Toán 9 Tập 1: Hãy tính

a) 2sin30^o - 2cos60^o + tg45^o;

b) sin45^o + cotg60^o.cos30^o;

c) cotg44^o.cotg45^o.cotg46^o.

Lời giải:

a) 2sin30^o - 2cos60^o + tg45^o = tg45^o = 1 (do sin30^o = cos60^o).

b) sin45^o + cotg60^o.cos30^o = (1+ √2)/2.

c) cotg44^o.cotg45^o.cotg46^o = cotg45^o = 1

(vì cotg44^o = tg46^o do 44^o + 46^o = 90^o mà tg46^o.cotg46^o = 1)

Bài 16 trang 110 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC có ∠A = 60^o. Chứng minh rằng: BC² = AB² + AC² – AB.AC.

Lời giải:

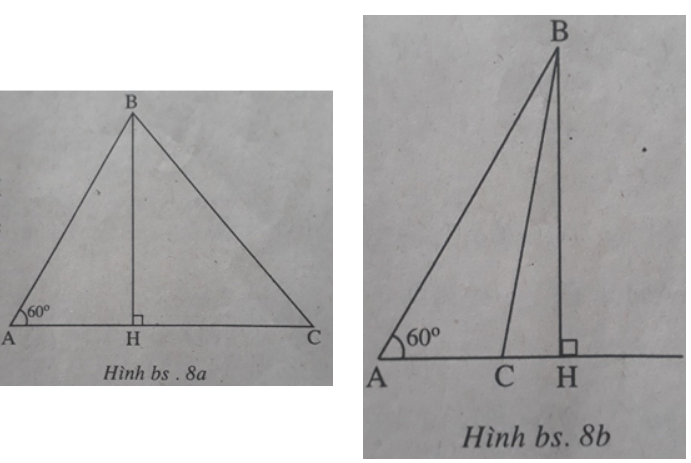
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để ∠(BAC) = 60^o là góc nhọn), do đó HC² = (AC-AH)²(xem h.bs.8a, 8b)

Công thức Py-ta-go cho ta

BC² = BH² + HC²

= BH² + (AC-AH)²

= BH² + AC² + AH² – 2AC.AH

= AB² + AC² – 2AC.AH.

Do ∠(BAC) = 60^o nên AH = AB.cos60^o = AB/2, suy ra BC² = AB² + AC² – AB.AC

Bài 17 trang 110 Sách bài tập Toán 9 Tập 1: Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo chứng minh rằng S_ABCD = 1/2 AC.BD.sinα.

Lời giải:

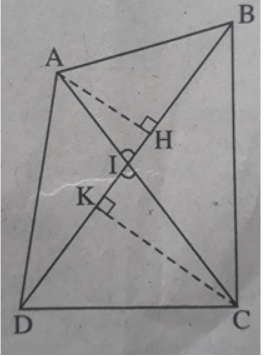
Giả sử hai đường chéo AC, BD cắt nhau tại I, ∠(AIB) = α là góc nhọn (xem h.bs.9)

Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.

Ta có: AH = AI.sinα, CK = CI.sinα,

Diện tích tam giác ABD là S_ABD = 1/2 BD.AH.

Diện tích tam giác CBD là S_CBD = 1/2 BD.CK.

Từ đó diện tích S của tứ giác ABCD là:

S = S_ABD + S_CBD = 1/2BD.(AH + CK)

= 1/2 BD.(AI + CI)sinα = 1/2BD.AC.sinα

Bài 18 trang 110 Sách bài tập Toán 9 Tập 1: Cho góc nhọn α

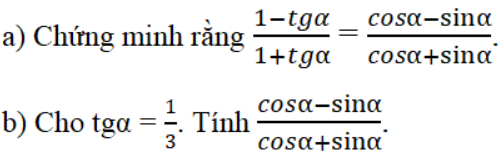
Lời giải:

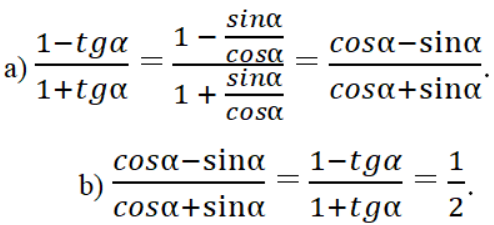
Bài 19 trang 110 Sách bài tập Toán 9 Tập 1: Tính giá trị của biểu thức

Lời giải:

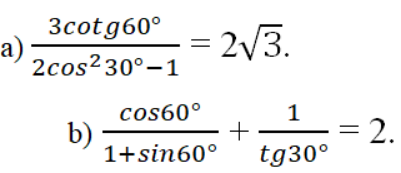
Bài 20 trang 110 Sách bài tập Toán 9 Tập 1: Trong hình thang vuông ABCD với các đáy AD, BC có ∠A = ∠B = 90^o, ∠(ACD) = 90^o. BC = 4cm, AD = 16cm. Hãy tìm các góc C và D của hình thang.

Lời giải:

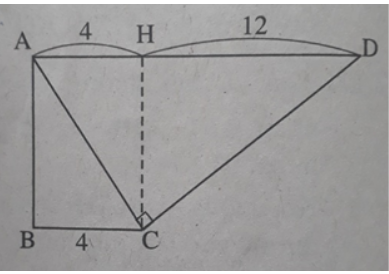
Kẻ đường cao CH của tam giác ACD vuông tại C. Khi đó

AH = BC = 4, HD = AD – AH = 12.

Từ đó

HC² = HA.HD = 48, vậy HC = 4√3.

Trong tam giác vuông HCD, ta có

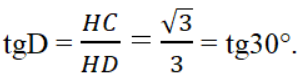
Nên ∠D = 30^o. Suy ra ∠(BCD) = 180^o - 30^o = 150^o.