Chứng minh rằng với mọi số phức z ≠ 1, ta có

Luyện tập (trang 190-191)

Haylamdo biên soạn và sưu tầm lời giải Bài 10 trang 190 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 10 (trang 190 sgk Giải Tích 12 nâng cao): Chứng minh rằng với mọi số phức z ≠ 1, ta có:

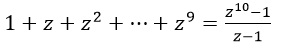
Lời giải:

Vì z ≠ 1, nên tính chất của số phức ta có đẳng thức cần chứng minh tương đương với :

(1+z+z²+⋯+z⁹ )(z-1)=z¹⁰-1

<=> z+z²+z³+⋯+z¹⁰-1-z-z²-z³-…-z⁹=z¹⁰-1

<=> z¹⁰-1=z¹⁰-1 (đpcm)

Vậy ta có điều cần chứng minh.