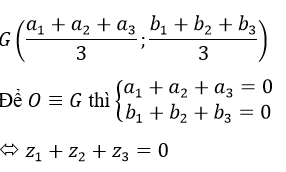Trong mặt phẳng phức, cho ba điểm A, B, C không thẳng hàng theo thứ tự

Luyện tập (trang 190-191)

Haylamdo biên soạn và sưu tầm lời giải Bài 15 trang 191 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 15 (trang 191 sgk Giải Tích 12 nâng cao):

a) Trong mặt phẳng phức, cho ba điểm A, B, C không thẳng hàng theo thứ tự biểu diễn các số phức z¹;z²;z³. Hỏi trọng tâm của tam giác ABC biểu diễn số phức nào?

b) Xét ba điểm A, B, C của mặt phẳng phức theo thứ tự biểu diễn ba số phức phân biệt z¹;z²;z³ thõa mãn |z¹ |=|z² |=|z³ |

Chứng minh rằng A, B, C là ba đỉnh của một tam giác đều khi và chỉ khi z¹+z²+z³=0

Lời giải:

Giả sử z₁=a₁+b₁ i => A(a₁;b₁)

z₂=a₂+b₂ i=>B(a₂;b₂)

z₃=a₃+b₃ i=>C(a₃;b₃)

a) Suy ra trọng tâm G của tam giác ABC là

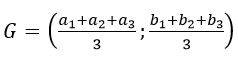
là điểm biểu diễn số phức :

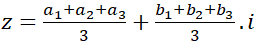
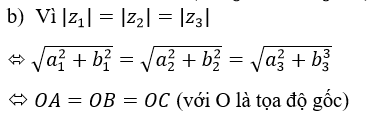
Vậy O là tâm đường tròn ngoại tiếp ΔABC. Để ΔABC là Δ đều thì O cũng là trọng tâm của ΔABC

Theo câu a) trọng tâm tam giác ABC là