Số dân của một thị trấn t năm kể từ năm 1970 ước tính bởi công thức

Luyện tập (trang 8-9)

Haylamdo biên soạn và sưu tầm lời giải Bài 10 trang 9 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 10 (trang 9 sgk Giải Tích 12 nâng cao):

Số dân của một thị trấn t năm kể từ năm 1970 ước tính bởi công thức

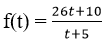
(f(t) được tính bằng nghìn người)

a. Tính số dân của thị trấn vào đầu năm 1908 và đầu năm 1995

b. Xem f là một hàm số xác định trên nửa khoảng [0; +∞). Tính f’(t) và xét chiều biến thiến của h trên nửa khoảng [0; +∞)

c. Đạo hàm của hàm số f biểu thị tốc độ tăng dần của thị trấn (tính bằng nghìn người/năm)

    + Tính tốc độ tăng dân số vào năm 1990 của thị trấn.

    + Tính tốc độ tăng dân số được dự kiến vào năm đầu 2008.

    + Vào năm nào thì tốc độ tăng dần số là 0,125 nghìn /người.

Lời giải:

a.Vào đầu năm 1980, ta có t = 10; f(10)=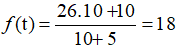

Vậy số dân của thị trấn vào đầu năm 1980 là 18 nghìn người.

Vào đầu năm 1995, ta có t = 25, f(25) = 22

Số dân của thị trấn vào đầu năm 1995 là 22 nghìn người.

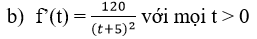
f(t) liên tục trên [0; +∞) (vì liên tục trên khoảng (-5; +∞))

vậy hàm số đồng biến trên [0; +∞)

c.

+ Tốc độ tăng dân số vào đầu năm 1990 là:

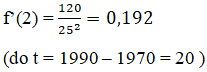
+ Tốc độ tăng dân số được dự kiến vào năm 2008 của thị trấn là:

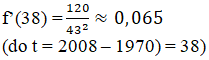
+ Ta có f’(t) = 0, 125

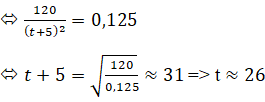
Vậy năm 1996, tốc độ tăng dân số của thị trấn là 0, 125 nghìn người / năm