Xét chiều biến thiên của hàm số sau: a) 1/3 x^3 - 2 x^2 + 4 x - 5

Luyện tập (trang 8-9)

Haylamdo biên soạn và sưu tầm lời giải Bài 6 trang 8 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 6 (trang 8 sgk Giải Tích 12 nâng cao): Xét chiều biến thiên của hàm số sau:

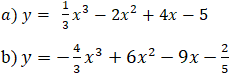
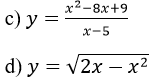
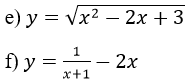
Lời giải:

a. Hàm số đã cho xác định trên R.

Đạo hàm: y'=x²-4x+4=(x-2)²≥0,∀x

Và y'=0 chỉ tại x = 2

Vậy hàm số đồng biến trên R.

b. Hàm số đã cho xác định trên R.

y'=-4x²+12x-9=-(2x-3)²≤0,∀x ∈R;y'=0 chỉ tại x=3/2

Vậy hàm số nghịch biến trên R.

c. Hàm số đã cho xác định trên D = R \ {5}

Đạo hàm

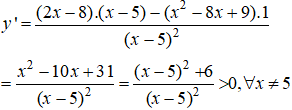
Nên hàm số đồng biến trên khoảng (-∞;5)và (5; +∞)

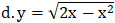
Tập xác định : D= [0; 2]

Hàm số đã cho liên tục trên đoạn [0; 2]

Đạo hàm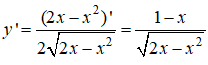

y’=0 ⇔ x=1

Bảng biến thiên:

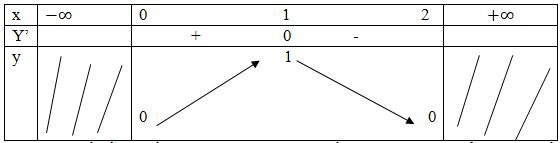
Vậy hàm số đồng biến trên [0; 1] và nghịch biến trên [1; 2] (có thể nói hàm số đồng biến trên (0; 1) nghịch biến trên (1; 2))

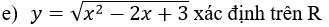
vì (x²-2x+3 = (x-1)²+2 > 0 ∀x ∈R)

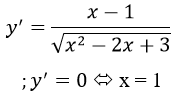
Bảng biến thiên

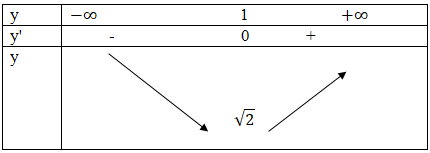
Hàm số nghịch biến trên (-∞;1), đồng biến trên (1; +∞)

f. Hàm số xác định trên D = R \ {-1}

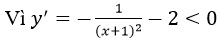
∀x ∈D nên hàm số nghịch biến trên mỗi khoảng (-∞; -1)và (-1; +∞)