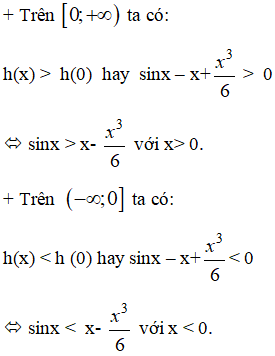Chứng minh bất đẳng thức sau: sin⁡x 0; sin x > x với mọi x < 0

Luyện tập (trang 8-9)

Haylamdo biên soạn và sưu tầm lời giải Bài 8 trang 8 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 8 (trang 8 sgk Giải Tích 12 nâng cao): Chứng minh bất đẳng thức sau:

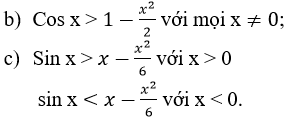
Lời giải:

a.

* Xét hàm số f(x) = x - sin⁡x hàm số này liên tục trên R.

+ Xét hàm số trên nửa khoảng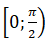

Đạo hàm f’(x) = 1 - cos⁡x > 0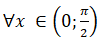

Do đó hàm số đồng biến trên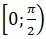

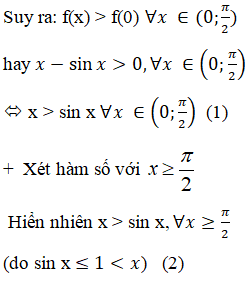
Từ (1) và (2) suy ra, x > sin x với x > 0.

** Xét hàm số y= x - sin x liên tục trên R.

+ Hàm số f(x) = x – sin x trên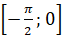

có đạo hàm f’(x) = 1 - cos x > 0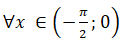

Do đó hàm số đồng biến trên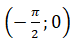

⇒ f(x) < f(0) hay x- sin x

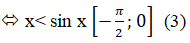
+ Hiển nhiên: x < sin x với mọi

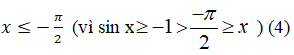
Từ(3) và (4) suy ra; x < sin x với mọi x < 0

b. Hàm số 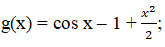xác định trên R và có đạo hàm g’(x) = x – sin x

Dựa vào ý a) và chú ý x- sin x = 0 ⇔ x = 0, ta có bảng biến thiên của hàm g(x)

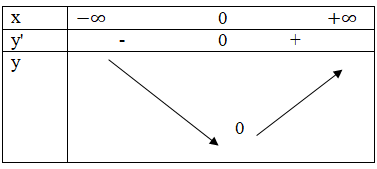
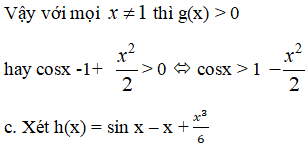
Tập xác định D = R và có đạo hàm

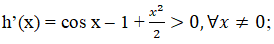
Suy ra, h(x) đồng biến trên R.