Tìm cực trị của các hàm số sau: 1/3x^3 + 2x^2 + 3x -1

Bài 2: Cực trị của hàm số

Haylamdo biên soạn và sưu tầm lời giải Bài 11 trang 16 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 11 (trang 16 sgk Giải Tích 12 nâng cao): Tìm cực trị của các hàm số sau:

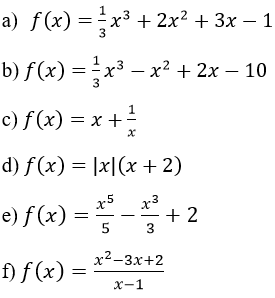
Lời giải:

a) Hàm số đã cho xác định trên R.

Ta có: f’(x) = x²+4x+3

Từ đó f’(x) = 0 ⇔ x = -1 hoặc x = -3

Cách 1.

Bảng biến thiên

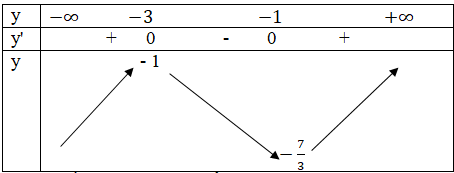
Vậy hàm số đạt cực đại tại điểm x = -3, giá trị cực đại của hàm số là: f_CĐ = f(-3) = -1.

Hàm số đạt cực tiểu tại điểm x = -1, giá trị cực tiển của hàm số là f_CT = f(-1) = -7/3

Cách 2. f’’(x) = 2x + 4 ⇒ f’’(-3) = -2 < 0; f’’(-1) = 2 > 0

Vậy hàm đạt cực đại tại điểm x = -3 giá trị cực đại của hàm số là:

f_CĐ = f(-3) = -1.

Hàm số đạt cực tiểu tại điểm x = -1, f_CT = f(-1) = -7/3

b) Tập xác định: R

f' (x)=x²-2x+2=(x-1)²+1>0,∀x ∈R=>f(x) luôn đồng biến nên hàm số không có cực trị.

c) Tập xác định: R \ {0}

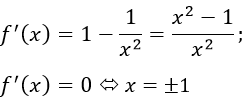
Cách 1.

Bảng biến thiên

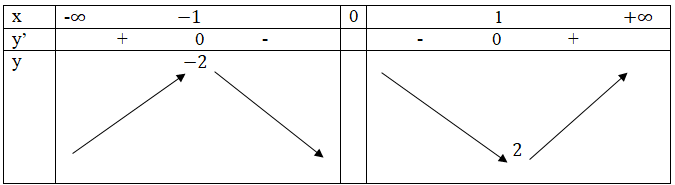
Vậy hàm số cực đại tại x = -1; f_CĐ=f(-1)=-2

Hàm số cực tiểu tại x = 1; f_CT=f(1)=2

Cách 2.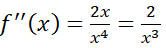

Vì f’’(- 1) = -2 < 0 nên hàm số đạt cực đại tại x = -1; f_CĐ = f(-1) = -2

f'' (1) = 2 > 0 nên hàm số đạt cực tiểu tại x = 1; f_CT = f(1) = 2

d) f(x) xác định liên tục trên R.

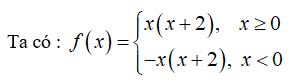
Với x > 0, f'(x) = 2x + 2

Từ đó f'(x) = 0 ⇔ x = -1 (loại)

Với x < 0, f'(x) = -2x - 2

Từ đó f'(x) = 0 ⇔ x = -1 (thỏa mãn)

Với x = 0, hàm số không có đạo hàm (chú ý sgk giải tích 12 nâng cao trang 12)

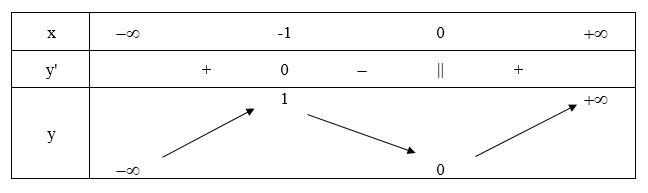
Hàm số đạt cực đại tại x = -1, f_CĐ = f(-1) = 1

Hàm số đạt cực tiểu tại x = 0, f_CT = f(0) = 0

Chú ý: mặc dù không tồn tại đạo hàm tại điểm , nhưng hàm số vẫn có thể đạt cực trị tại điểm này.

e) Tập xác định D = R

f’(x) = x⁴-x²

f' (x)=0 ⇔ x = 0 hoặc x = ±1

Bảng biến thiên:

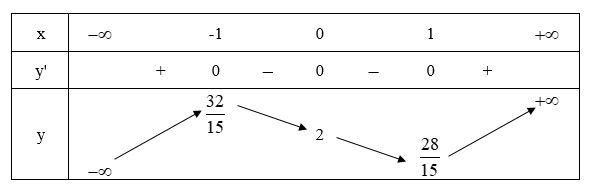
Vậy hàm số đạt cực đại tại x = -1, f_CD = f(-1) = 32/15 và hàm số cực tiểu tại x = 1; f_CT = f(1) = 28/15

f) Tập xác định D = R \ {1}

Ta có:

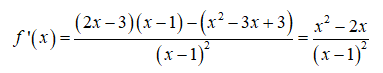
f'(x)=0 ⇔ x = 0 hoặc x = 2. Ta có bảng biến thiên:

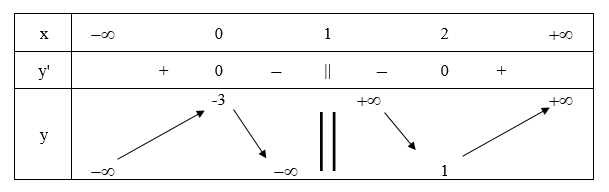
Vậy hàm số cực đại tại x = 0, f_CĐ = f(0) = -3 và hàm số cực tiểu tại x = 2; f_CT = f(2) = 1