Tìm các hệ số a, b, c, d của hàm số f(x) = ax^3+bx^2+cx+d sao cho hàm số đạt cực tiểu tại điểm x = 0

Bài 2: Cực trị của hàm số

Haylamdo biên soạn và sưu tầm lời giải Bài 13 trang 17 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 13 (trang 17 sgk Giải Tích 12 nâng cao): Tìm các hệ số a, b, c, d của hàm số f(x) = ax³+bx²+cx+d sao cho hàm số đạt cực tiểu tại điểm x = 0; f(0) = 0 đạt cực đại tại điểm x = 1, f(1) = 1

Lời giải:

Ta có f’(x) = 3ax²+2bx+c ⇒ f' (0)=c;f' (1)=3a+2b+c

Vì f(0) = 0 ⇒ d= 0

Hàm số đạt cực tiểu tại x = 0 nên f’(0) = 0 ⇒ c =0; f(1) = a + b = 1

Hàm số đạt cực đại tại điểm x = 1 nên f’(1) = 0 ⇒ 3a + 2b = 0

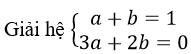
ta được a = -2; b = 3

Vậy f(x) = -2x³+3x²

Thử lại f’(x) = -6x²+6x;f'' (x)=-12x+6

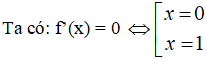
f’(0) > 0. Hàm số đạt cực tiểu tại điểm x = 0

f’(1) = -6 < 0. Hàm số đạt cực đại tại x = 1

Đáp số: a = -2; b = 3; c = 0 ; d = 0