Độ giảm huyết áp của một bệnh nhân được cho bởi công thức G(x) = 0,025x^2 (30-x)

Luyện tập (trang 23-24)

Haylamdo biên soạn và sưu tầm lời giải Bài 23 trang 23 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 23 (trang 23 sgk Giải Tích 12 nâng cao): Độ giảm huyết áp của một bệnh nhân được cho bởi công thức G(x) = 0,025x² (30-x). Trong đó x là liếu lượng thuốc được tiêm cho bệnh nhận (x lấy đơn vị là miligam). Tính liều lượng thuộc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất và tính độ giảm đó.

Lời giải:

Ta có G(x) = 0,75x²-0,025x³;

G' (x) = 1,5x-0,075x²; G(x)' = 0 ⇔ x = 0; x = 20

Bảng biến thiên.

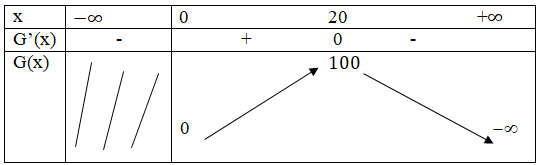
max_{x > 0}G(x) = G(20) = 100

Vậy liều lượng cần tiêm cho bệnh nhân huyết áp giảm nhiều nhất là 20mg.

Khi đó, độ giảm huyết áp là 100

Vậy liều lượng cần tiêm cho bệnh nhân huyết áp giảm nhiều nhất là 20mg. khi đó, độ giảm huyết áp là 100.