Cho parabol (P) y = x^2 và điểm A(-3; 0). Xác định điểm M thuộc Parabol (P)

Luyện tập (trang 23-24)

Haylamdo biên soạn và sưu tầm lời giải Bài 24 trang 23 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 24 (trang 23 sgk Giải Tích 12 nâng cao):Cho parabol (P) y = x² và điểm A(-3; 0). Xác định điểm M thuộc Parabol (P) sao cho khoảng cách AM ngắn nhất và tìm khoảng cách ngắn nhất đó.

Lời giải:

Gọi M(x; x²) là một điểm bất kì trên (P).

Ta có: AM² = (x+3)² +(x²)² = x⁴ + x² + 6x + 9

AM nhỏ nhất ⇔ f(x) = x⁴ + x² + 6x + 9 đạt giá trị nhỏ nhất.

f'(x) = 4x³ + 2x + 6 = (x+1)(4x² - 4x + 6)

f'(x) = 0 ⇔ x = -1

Bảng biến thiên

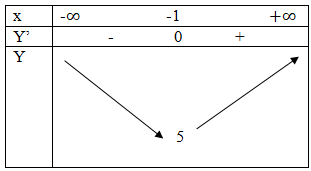
Dựa vào bảng biến thiên suy ra, hàm số đạt nhỏ nhất tại điểm x = -1; f(-1) = 5.

Suy ra, khoảng cách AM đạt giá trị nhỏ nhất khi tọa độ điểm M (-1; 1). Lúc đó AM = √5