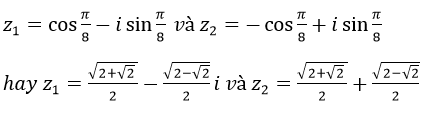Dùng công thức lượng giác để chứng minh rằng với mọi số thức φ, ta có

Luyện tập (trang 199)

Haylamdo biên soạn và sưu tầm lời giải Bài 26 trang 199 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 26 (trang 199 sgk Giải Tích 12 nâng cao):

a) Dùng công thức lượng giác để chứng minh rằng với mọi số thức φ, ta có:

(cos⁡φ+i sin⁡φ )²=cos⁡2φ+isin 2φ

Từ đó hãy tìm mọi căn bậc hai của số thức: cos⁡2φ+isin 2φ. Hãy so sánh cách giải thích này với cách giải thích học ở bài §2.

Lời giải:

a) Ta có: (cos⁡φ+i sin⁡φ )²=(cos²⁡φ-sin²⁡φ )+2sinφcosφi=cos⁡2φ+isin 2φ

Suy ra cos⁡2φ+isin 2φ có căn bậc hai là:

cos⁡φ+i sin⁡φ và -cos⁡φ-i sin⁡φ

nhận xét: các giải thích này rất thuận lợi cho việc tìm căn bậc hai của số phức: z=a+bi với a²+b²=1

Ta có:

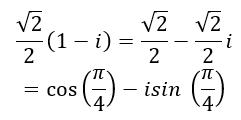
Theo câu a) thì số cos⁡(π/4)-i sin⁡(π/4) có căn bậc hai là: