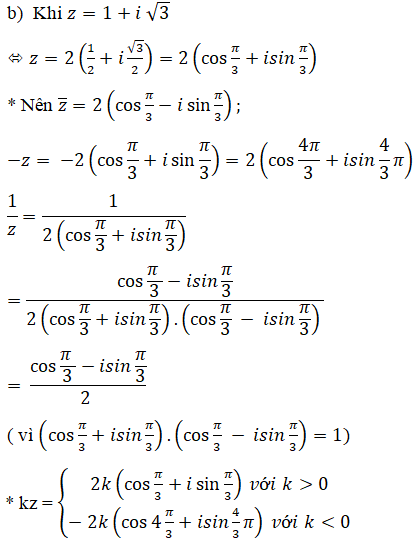Hãy tìm dạng lượng giác của các số phức trang 205 sgk Giải Tích 12 nâng cao

Bài 3: Dạng lượng giác của số phức và ứng dụng

Haylamdo biên soạn và sưu tầm lời giải Bài 27 trang 205 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 27 (trang 205 sgk Giải Tích 12 nâng cao): Hãy tìm dạng lượng giác của các số phức: z−; -z;1/z;kz (k ∈R^*) trong mỗi trường hợp sau:

a) z=r(cos⁡φ+isin φ)(r>0)

b) z=1+i √3

Lời giải:

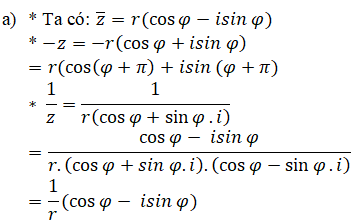
Kz là một số phức có modun là |Kz| = |K|. |z| = |K|.r, có acgumen là φ nếu K > 0, là φ+π nếu k < 0.

Vậy Kz = |K|.r(cos⁡φ+isin φ) nếu k > 0

Kz = |K|r. (cos⁡(φ+π)+isin (φ+π) nếu k < 0