Cho hàm số y = -x4 + 2mx2 - 2m + 1 (m tham số) có đồ thị là Cm

Toán lớp 12 Bài ôn tập chương I

Bài 10 (trang 46 SGK Giải tích 12): Cho hàm số

y = -x⁴ + 2mx² - 2m + 1 (m tham số)

có đồ thị là (C_m).

a) Biện luận theo m số cực trị của hàm số.

d) Với giá trị nào của m thì (C_m) cắt trục hoành?

c) Xác định để (C_m) có cực đại, cực tiểu.

Lời giải:

a) y' = -4x³ + 4mx = 4x(m - x²)

y' = 0 ⇔ 4x(m - x²) = 0 ⇔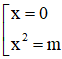

y’’ = -12x² + 4m.

- Nếu m ≤ 0, phương trình y’ = 0 có nghiệm duy nhất x = 0.

Mà y’’(0) = 4m < 0

⇒ x = 0 là điểm cực đại và là cực trị duy nhất của hàm số.

- Nếu m > 0 thì phương trình (1) có 2 nghiệm phân biệt khác 0 nên phương trình y’= 0 có 3 nghiệm

⇒ hàm số có 3 cực trị.

b) – Xét m ≤ 0, phương trình y’ = 0 có nghiệm duy nhất x = 0.

Ta có bảng biến thiên :

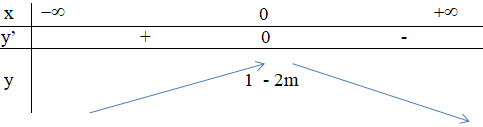
(C_m) cắt trục hoành ⇔ 1 – 2m ≥ 0

⇔ m ≤ 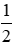(thỏa mãn với mọi m ≤ 0) (1)

- Xét m > 0, phương trình y’ = 0 có 3 nghiệm 0 ;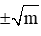

Ta có bảng biến thiên :

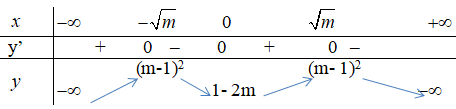
(C_m) cắt trục hoành ⇔ (m – 1)² ≥ 0 (thỏa mãn với mọi m) (2)

Kết hợp (1) và (2) suy ra (C_m) cắt trục hoành với mọi m ∈ R.

c) Dựa vào bảng biến thiên phần b) ta có :

(C_m) có cực đại, cực tiểu ⇔ m > 0