Tính diện tích hình phẳng giới hạn bởi đường cong y = x2+1

Toán lớp 12 Bài 3 : Ứng dụng của tích phân trong hình học

Bài 2 (trang 121 SGK Giải tích 12): Tính diện tích hình phẳng giới hạn bởi đường cong y = x²+1 , tiếp tuyến với đường này tại điểm M(2; 5) và trục Oy.

Lời giải:

Xét hàm số y = x² + 1 có đạo hàm y’ = 2x

Phương trình tiếp tuyến với đường cong y = x² + 1 tại điểm M(2; 5) là :

y = y’(2).(x – 2) + 5 ⇔ y = 4(x- 2) + 5 hay y = 4x - 3

Phương trình hoành độ giao điểm của đường cong và tiếp tuyến là :

x² + 1 = 4x – 3 ⇔ x² - 4x + 4 = 0 ⇔ x= 2

Vậy diện tích hình giới hạn bởi y = x² + 1; tiếp tuyến y = 4x – 3 và trục Oy (x = 0) là:

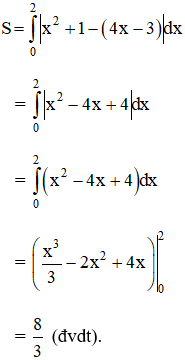
Kiến thức áp dụng

+ Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) ; y = g(x) và hai đường thẳng x = a ; x = b là :

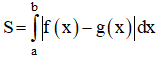
+ Phương trình tiếp tuyến của đường cong y = f(x) tại điểm M(x₀ ; y₀) là :

y = f’(x₀).( x- x₀) + y₀