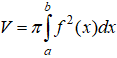Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox
Toán lớp 12 Bài 3 : Ứng dụng của tích phân trong hình học
Bài 5 (trang 121 SGK Giải tích 12): Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt 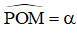
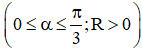
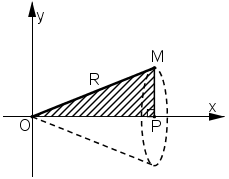
Gọi V là khối tròn xoay thu được khi quay tam giác đó quanh trục Ox (H.63).
a) Tính thể tích của V theo α và R.
b) Tìm α sao cho thể tích V lớn nhất.
Lời giải:
a) Ta có: OP = OM.cosα = R. cosα
Phương trình đường thẳng OM đi qua O nên có dạng: y = k.x
OM tạo với trục hoành Ox 1 góc
⇒ Hệ số góc k = tanα
⇒ OM: y = x.tanα
Vậy khối tròn xoay được tạo bởi hình phẳng giới hạn bởi đường thẳng y = x.tanα; y = 0; x = 0; x = R.cosα quay quanh trục Ox
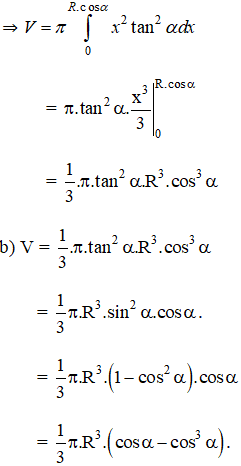
* Ta tìm giá trị lớn nhất của P = cosα – cos3α
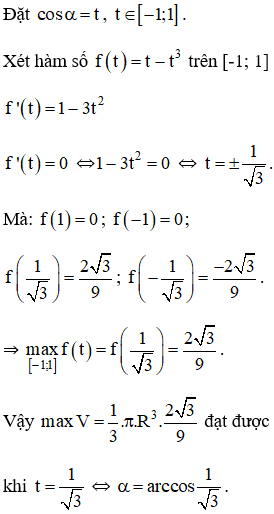
Kiến thức áp dụng
+ Đường thẳng đi qua gốc tọa độ có dạng: y = kx.
Trong đó, k là hệ số góc và k = tan α với α là góc tạo bởi đưởng thẳng và tia Ox.
+ Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y = f(x); trục Ox và hai đường thẳng x= a và x = b (a < b) là: