Chứng minh rằng với mọi giá trị của tham số m, hàm số y = x3 - mx2 - 2x + 1
Toán lớp 12 Bài 2: Cực trị của hàm số
Bài 4 (trang 18 SGK Giải tích 12): Chứng minh rằng với mọi giá trị của tham số m, hàm số
y = x3 - mx2 - 2x + 1
luôn luôn có một cực đại và một điểm cực tiểu.
Lời giải:
TXĐ: D = R
+ y' = 3x2 - 2mx – 2
y’ = 0 ⇔ 3x2 – 2mx – 2 = 0 ⇔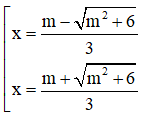 
+ y’’ = 6x – 2m.
⇒ 
là một điểm cực đại của hàm số.
⇒ 
là một điểm cực tiểu của hàm số.
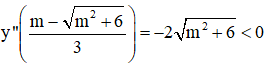
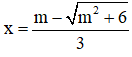
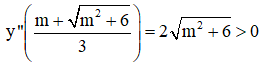
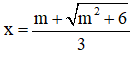
Vậy hàm số luôn có 1 điểm cực đại và 1 điểm cực tiểu.
Kiến thức áp dụng
Xét y = f(x) có đạo hàm cấp hai trong khoảng (x0 – h ; x0 + h), h > 0.
+ f’(x0) = 0 và f’’(x0) > 0 thì x0 là điểm cực tiểu.
+ f’(x0) = 0 và f’’(x0) < 0 thì x0 là điểm cực đại.
