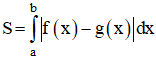Tính diện tích hình phẳng giới hạn bởi các đường

Toán lớp 12 Bài 3 : Ứng dụng của tích phân trong hình học

Bài 1 (trang 121 SGK Giải tích 12): Tính diện tích hình phẳng giới hạn bởi các đường:

a) y = x²;y = x + 2

b) y =|lnx|; y = 1

c) y = (x - 6)²; y = 6x - x²

Lời giải:

a) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình :

x² = x + 2 ⇔ x² – x – 2 = 0 ⇔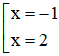

Vậy diện tích cần tìm là:

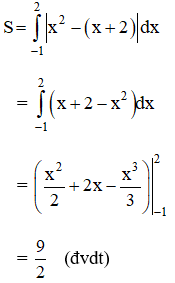
b) Hoành độ giao điểm hai đồ thị là nghiệm của pt :

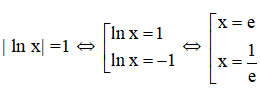
Vậy diện tích cần tìm là:

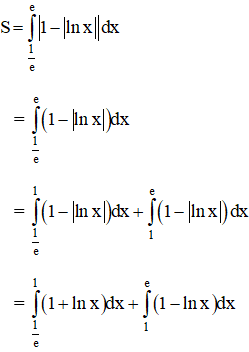
(Vì lnx > 0 khi 1 < x < e và lnx < 0 khi ).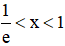

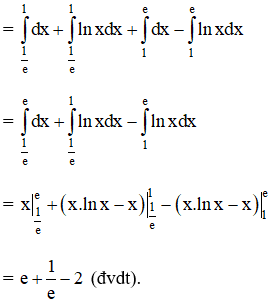
c) Hoành độ giao điểm của hai đồ thị là nghiệm của pt :

(x - 6)² = 6x - x²

⇔ (x – 6)² + x² – 6x = 0

⇔ (x - 6). (x - 6+ x) = 0

⇔ (x - 6)(2x - 6) = 0

⇔ x = 3 hoặc x = 6

Vậy diện tích cần tìm là:

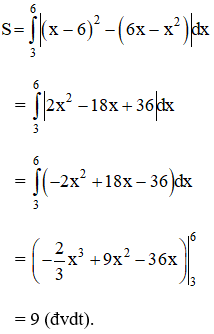
Kiến thức áp dụng

+ Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) ; y = g(x) và hai đường thẳng x = a ; x = b là :