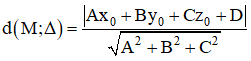Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0

Toán lớp 12 Bài 3 : Phương trình đường thẳng trong không gian

Bài 8 (trang 91 SGK Hình học 12): Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0

a)Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α).

b)Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng (α).

c)Tính khoảng cách từ M đến mp(α).

Lời giải:

a) Đường thẳng MH vuông góc với (α)

⇒ MH nhận vtpt của (α) 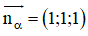là 1 vtcp

Mà M(1; 4; 2) ∈ MH

⇒ Pt đường thẳng MH: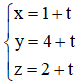

⇒ H(1 + t; 4 + t; 2 + t).

H ∈ (α) ⇒ 1 + t + 4 + t + 2 + t – 1 = 0 ⇔ t = -2.

⇒ H(-1; 2; 0).

b) M’ đối xứng với M qua (α)

⇒ H là trung điểm MM’

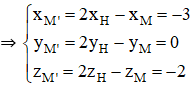
⇒ M’(-3; 0; -2).

c) Khoảng cách từ M đến mặt phẳng (α) là:

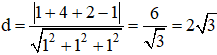
Kiến thức áp dụng

+ Tìm hình chiếu H của điểm M trên mặt phẳng (Δ): Ax + By + Cz + D = 0

Phương trình đường thẳng MH đi qua M và vuông góc với Δ

⇒ MH nhận vtpt của Δ là (A; B; C) là 1 vtpt

⇒ viết phương trình MH.

⇒ tìm tọa độ H là giao điểm của MH và (Δ).

+ Khoảng cách từ M(x0 ; y0 ; z0) đến (Δ): Ax + By + Cz + D = 0