Giáo án Toán 9 Bài 2: Hàm số bậc nhất mới nhất
Giáo án Toán 9 Bài 2: Hàm số bậc nhất mới nhất
I. Mục tiêu:
Qua bài này giúp HS:
1. Kiến thức
- Trả lời được các câu hỏi của bài toán mở đầu, qua đó nhận biết được hàm số bậc nhất.
- HS lấy được ví dụ về hàm số bậc nhất.
- HS xác định được tính tăng, giảm của hàm số bậc nhất. Qua đó giải thích được vì sao một hàm bậc nhất cho trước là hàm đồng biến, nghịch biến.
- HS phân biệt được tính đồng biến, nghịch biến của một hàm bậc nhất nhờ nhận xét về hệ số a.
2. Kỹ năng
- Phân loại được hệ số a âm hay dương, qua đó kết luận tính đồng biến, nghịch biến của một hàm số bậc nhất.
- Rèn kĩ năng trình bày bài tập chính xác.
3. Thái độ
- Nghiêm túc và hứng thú học tập
4. Định hướng năng lực, phẩm chất
- Năng lực tính toán
- Năng lực giải quyết vấn đề
- Năng lực hợp tác.
- Năng lực ngôn ngữ
- Năng lực giao tiếp.
- Năng lực tự học.
* Phẩm chất: Tự tin, tự lực
II. Chuẩn bị:
- Gv : Giáo án, sách, phấn mầu, bảng nhóm.
- Hs: Đồ dùng học tập, đọc trước bài.
III. Phương tiện và đồ dùng dạy học
Thước, bút dạ, bảng phụ, bảng nhóm.
IV. Tiến trình dạy học:
1. Ổn định :(1 phút)
A. Hoạt động khởi động (5 phút).
Kiểm tra bài cũ :
Hàm số là gì? Hãy điền vào chỗ trống trong các câu sau:
+ Nếu x1 < x2 mà f(x1) < f(x2) thì hàm số y = f(x) .......... trên R.
+ Nếu x1 < x2 mà f(x1) < f(x2) thì hàm số y = f(x).......... trên R.
HS trả lời – GV nhận xét, cho điểm ( ĐN: SGK - đồng biến / nghịch biến)
GV ĐVĐ: Ta đã biết khái niệm hàm số và biết lấy ví dụ về hàm số được cho bởi công thức. Hôm nay ta sẽ học một hàm số cụ thể, đó là hàm số bậc nhất. Vậy hàm số bậc nhất là gì, nó có tính chất như thế nào, đó là nội dung bài hôm nay.
B. Hoạt động hình thành kiến thức
| Giáo viên | Học sinh | Nội dung ghi bài | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Hoạt động 1: Khái niệm về hàm sốbậc nhất ( 15 phút) - Mục tiêu: HS định nghĩa được một hàm số là hàm bậc nhất, nhận biết được hàm số bậc nhất qua các ví dụ. - Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp - Kĩ thuật sử dụng: Kĩ thuật động não. - Năng lực: Tính toán, giải quyết vấn đề. |
||||||||||||
|
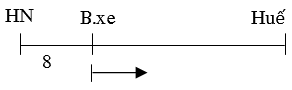
GV tóm tắt bài toán bằng sơ đồ ? Bài toán cho biết gì? Yêu cầu làm gì? ? Với vận tốc như vậy sau một giờ đi được bao nhiêu km? ? Sau t giờ đi được bao nhiêu km? ? Vậy sau t giờ thì ô tô cách trung tâm Hà Nội bao nhiêu km? Cho HS dựa vào công thức đó điền số liệu vào bảng phụ ? Vì sao s là hàm số của t? (Vì mỗi giá trị của x ta đều tính được 1 giá trị duy nhất của y) ? Bậc của đa thức 50t + 8 là bao nhiêu ? Từ đó giáo viên đưa ra nội dung của hàm số bậc nhất Chú ý cho HS trường hợp b = 0 hàm số có dạng y = ax Cho hs nhận diện khái niệm bằng bài tập: đẳng thức nào dưới đây biểu thị một hàm số bậc nhất ? hãy chỉ rõ a và b trong các hàm số ấy. a, y = -4x + 5 b, y = x2 - 3x + 1 c, y = 0x - 4 d, y = 1 + √5x e, y = 1 + √5x g, y = 1 h, y = i) y = √2(x - 1) + √3 |
HS đọc nội dung bài toán Thực hiện ?1 HS đứng tại chỗ điền HS tính toán sau đó điền số liệu vào bảng phụ để hoàn thành ?2 HS suy nghĩ và trả lời. - Bậc nhất HS nhắc lại định nghĩa HS đứng tại chỗ trả lời |
1. Khái niệm về hàm số bậc nhất. Bài toán: SGK/46
? Sau t(h) ôtô cách trung tâm HN bao nhiêu km Sau 1 giờ ô tô đi được 50(km. ) Sau t giờ ô tô đi được 50t (km) Sau t giờ ô tô cách trung tâm Hà Nội là s = 50t + 8 (km)
s là hàm số của t vì: – s phụ thuộc vào t – ứng với mỗi giá trị của t chỉ có một giá trị của s. Định nghĩa: Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước và a ≠ 0 Chú ý: Khi b = 0, hàm số có dạng y = ax Bài tập: Hàm số bậc nhất là y = -4x + 5 với a = -4; b = 5 y = 1 + √5 với a = √5; b = 1 y = y = √2(x + 1) + √3 với a = √2, b = √3 - √2 |
||||||||||
|
Hoạt động 2: Tính chất( 15 phút) - Mục tiêu: HS chứng minh được hàm số y=3x+1 là hàm số đồng biến, qua đó khái quát được thành tính đồng biến, nghịch biến của một hàm số bằng tính chất. - Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp - Kĩ thuật sử dụng: Kĩ thuật động não. - Năng lực: Tính toán, giải quyết vấn đề. |
||||||||||||
Cho HS tự đọc ví dụ trong SGK sau đó trả lời các câu hỏi sau: ? Hàm số y = -3x + 1 xác định với những giá trị nào của x? ? Chứng minh rằng hàm số y = -3x + 1 nghịch biến trên R Cho HS làm ?3 theo nhóm GV gọi đại diện lên bảng trình bày các nhóm còn lại nhận xét và bổ sung GV nhận xét và đánh giá hoạt động nhóm ?Vậy hàm số y = f(x) = ax + b đồng biến khi nào? nghịch biến khi nào Dựa và câu trả lời của HS GV giới thiệu tính chất của hàm số bậc nhất. |
HS đọc ví dụ trong SGK sau đó trả lời các câu hỏi trên HS làm ?3 theo nhóm trong 5 phút. Đại diện một nhóm lên trình bày các nhóm còn lại nhận xét và bổ sung HS suy nghĩ và trả lời. HS nhắc lại tính chất của hàm số bậc nhất. |
2. Tính chất: Ví dụ: Xem SGK/47 ?3 Với x1, x2 ∈ R và x1 < x2 ta có: f(x1) = 3x1 + 1 ; f(x2) = 3x2 + 1 Khi đó: f(x2) - f(x1) = (3x2 + 1) - (3x1 + 1) = 3(x2 - x1) < 0 nên f(x2) < f(x1) Vậy hàm số y = 3x + 1 đồng biến trên R Tổng quát: Hàm số y = ax + b xác định với mọi R + a > 0 => h/s đồng biến trên R + a < 0 => h/s nghịch biến trên R |
||||||||||
|
B - Hoạt động luyện tập- vận dụng – 7 phút - Mục tiêu: HS vận dụng được định nghĩa, tính chất giải các bài tập có liên quan. - Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp - Kĩ thuật sử dụng: Kĩ thuật động não. - Năng lực: Tính toán, giải quyết vấn đề. |
||||||||||||
| Cho HS lấy ví dụ về hàm số đồng biến và nghịch biến Gv yêu cầu hs giải thích vì sao hàm số ĐB? Vì sao hàm số nghịch biến ? Cho hàm số y = (m - 2)x + 3; (m - 2 ≠ 0) Với giá trị nào của m thì hàm số ĐB? NB? |
HS lấy ví dụ về hàm số đồng biến và nghịch biến |
a/Hàm số đồng biến: y = 5x + 3, y = 3x + 2, ... b/ Hàm số nghịch biến: y = -5x + 3, y = -7x + 6 , y = -3x + 2 Bài tập m - 2 > 0 <=> m > 2 thì HS đồng biến m < 2 thì hàm số nghịch biến |
||||||||||
|
C – Tìm tòi mở rộng – 1 phút - Mục tiêu: - HS chủ động làm các bài tập về nhà để củng cố kiến thức đã học. - HS chuẩn bị bài mới giúp tiếp thu tri thức sẽ học trong buổi sau. - Kĩ thuật sử dụng: Kĩ thuật viết tích cực - Năng lực: Giải quyết vấn đề. |
||||||||||||
| Bài tập về nhà: 8,9,10,11/48 SGK; 6,7,8,9/57 SBT. Học thuộc khái niệm và tính chất của hàm số bậc nhất. Chuẩn bị tiết luyện tập |
||||||||||||

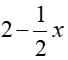
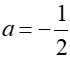 ; b = 2
; b = 2