Giáo án Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây mới nhất
Giáo án Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây mới nhất
I. Mục tiêu:
Qua bài này giúp HS:
1. Kiến thức
- Phát biều được các định lí về liên hệ giữa dây và khoảng cách từ tâm đến dây của một đường tròn.
- Vận dụng được các định lí để so sánh độ dài hai dây, so sánh các khoảng cách từ tâm đến dây.
- Suy luận để chứng minh logic.
2. Kỹ năng
- Vận dụng được các khái niệm của bài học để giải các bài tập có liên quan.
- Rèn được kĩ năng trình bày bài toán chứng minh, chính xác trong suy luận. Rèn tính cẩn thận, rõ ràng.
3. Thái độ
- Nghiêm túc và hứng thú học tập.
4. Định hướng năng lực
- Năng lực tính toán,
- Năng lực giải quyết vấn đề,
- Năng lực hợp tác.
- Năng lực ngôn ngữ.
- Năng lực giao tiếp.
- Năng lực tự học.
* Phẩm chất: Tự tin, tự chủ
II. Chuẩn bị:
- Gv : Giáo án, sách, phấn mầu, bảng nhóm,
- Hs: Đồ dùng học tập, đọc trước bài.
III. Phương tiện và đồ dùng dạy học
- Thước, bút dạ, bảng phụ, bảng nhóm, máy chiếu
IV. Tiến trình dạy học:
1.Ổn định :1 phút
2.Kiểm tra bài cũ : (Kết hợp trong bài)
3.Bài mới :
| Giáo viên | Học sinh | Nội dung ghi bài |
|---|---|---|
|
A - Hoạt động khởi động – 12p - Mục tiêu: HS phát biểu được bài toán, chứng minh và trình bày lại được cách chứng minh bài toán, qua đó nhận xét về mối liên hệ giữa dây và khoảng cách từ tâm đến dây. - Phương pháp: Vấn đáp, trực quan, quan sát. - Kĩ thuật sử dụng: Kĩ thuật động não |
||
Ta biết đường kính là dây lớn nhất của đường tròn. Vậy có 2 dây của đường tròn thì dựa vào cơ sở nào để chúng ta so sánh chúng. Bài học hôm nay chúng ta sẽ tìm hiểu Ta xét bài toán sgk. Nếu một trong hai dây là đường kính thì kết luận có đúng không? |
Học sinh nghe và ghi bài Một em đọc đề bài toán, hs vẽ hình Học sinh phát biểu cách chứng minh. HS: Giả sử CD là đường kính => K Ξ O => KO=0, KD=R => OK2+KD2=R2 = OH2+HB2 Vậy kết kluận trên vẫn đúng |
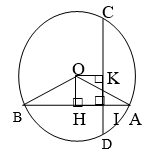
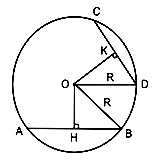
1. Bài toán:
Giải:
Ta có: OK ⊥ CD tại K OH ⊥ AB tại H Áp dụng định lí Pitago vào ∆OHB và ∆OKD ta có: OH2 + HB2 = OB2 = R2 (1) OK2 + KD2 = OD2 = R2 (2) Từ (1) và (2) suy ra OH2 + HB2 = OK2 + KD2 *Chú ý: Kết luận trên vẫn đúng nếu 1 hoặc hai dây là đường kính |
|
B - Hoạt động hình thành kiến thức- 17p Liên hệ giữa dây và khoảng cách từ tâm đến dây - Mục tiêu: HS trả lời được câu hỏi ở ?1 và ?2, qua đó phát biểu được 2 định lí. - Phương pháp: Nêu vấn đề, vấn đáp, trực quan. - Kĩ thuật sử dụng: Kĩ thuật động não, kĩ thuật hỏi và trả lời. - Năng lực: Tính toán, giải quyết vấn đề. |
||
(Hoạt động nhóm) Từ kết quả của bài toán. OK2 + KD2 = OH2 + HB2 Hãy chứng minh rằng: NV1: a) AB = CD thì OH=OK. NV2: b) OH = OK thì AB = CD. Yêu cầu học sinh tự chứng minh câu b tương tự như câu a Qua bài toán này chúng ta rút ra nhận xét gì? Nêu bài toán: Cho AB, CD là hai dây (O), OH ⊥ AB; OK ⊥ CD chứng minh rằng a) Nếu AB > CD thì OH < OK. b) Nếu OH < OK thì AB > CD Từ hai nhận xét trên ta có định lý 2 |
Học sinh thảo luận 1 HS lên bảng làm Học sinh phát biểu Một học sinh đọc định lý 1 sgk, Qua bài toán học sinh rút ra nhận xét: Trong một đường tròn hoặc hai đường tròn bằng nhau dây nào lớn hơn thì khoảng cách từ tâm đến dây đó nhỏ hơn. Một học sinh đọc nội dung định lý 2 sgk. |
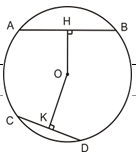
2. Liên hệ giữa dây và khoảng cách từ tâm đến dây. a) OH ⊥ AB; OK ⊥ CD, theo định lý 1 ta có.
=> HB = KD => HB2 = KD2 mà OH2 + HB2 = OK2 + KD2 => OH2 = OK2 OH = OK b) Chứng minh tương tự (học sinh tự làm) Định lý 1:Trong đường tròn (O) AB=CD <=> OH=OK Bài toán: a) OH AB; OK CD, theo định lý 1 ta có.
Nếu AB >CD => => HB > KD => HB2 > KD2 Mà OH2 + HB2 = OK2 + KD2 => OH2 < OK2 OH < OK b) Chứng minh tương tự. Định lý 2: Trong đường tròn (O) AB > CD <=> OH < OK |
|
C - Hoạt động luyện tập – Vận dụng – 12p - Mục tiêu: - HS vận dụng được kiến thức đã học để làm bài tập trắc nghiệm điền khuyết. PP: Thuyết trình, vấn đáp |
||
| Yêu cầu học sinh làm ?3 (Hoạt động cá nhân). Cho học sinh đọc đề ra và phát biểu cách làm bằng miệng sau đó giáo viên ghi lên bảng. Vận dụng Bài 12: NV1: ? Ta có thể thay câu c/m CD=AB bởi câu nào khác NV2: ? Từ I kẻ dây MI ⊥ OI. So sánh MN với AB ? Qua bài học chúng ta cần ghi nhớ những kiến thức gì |
Học sinh đứng tại chỗ trả lời miệng
Một học sinh đọc to đề ra và nêu giả thiết kết luận. (k/c từ O đến 2 dây AB và CD bằng nhau). Học sinh thảo luận trên lớp và nêu cách giải. |
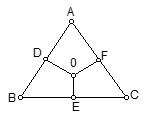
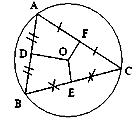
?3 a) O là giao điểm của các đường trung trực của tam giác ABC suy O là tâm của đường tròn ngoại tiếp tam giác ABC.
Có OE = OF suy ra AC = BC (đlý 1) b) OD > OE và OE = OF => OD > OF => AB < AC (đlý2) Bài 12 sgk
a) Kẻ OH ⊥ AB tại H, ta có: AH = HB = AB:2 = 8:2 = 4 cm. Tam giác vuông OHB có OB2 = BH2 + OH2 ( định lý pi ta go). Suy ra OH = 3cm. b)Kẻ OK ⊥ CD => tứ giác OHIK là hình chữ nhật => OK = IH = 4-1 = 3cm. Ta có OH = OK suy ra: AB = CD (định lý liên hệ giữa dây và k/c đến tâm) |
|
D - Hoạt động Tìm tòi, mở rộng – 1p - Mục tiêu: - HS chủ động làm các bài tập về nhà để củng cố kiến thức đã học. - HS chuẩn bị bài mới giúp tiếp thu tri thức sẽ học trong buổi sau. - Kĩ thuật sử dụng: Kĩ thuật viết tích cực - Năng lực: Giải quyết vấn đề, năng lực tự học. |
||
|
+ Về nhà đọc thuộc các định lý đã học . + Làm các bài tập 13,15,16 SGK . Chuẩn bị tiết Luyện tập |
||

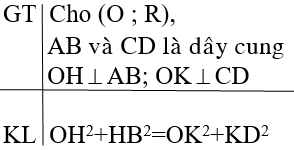
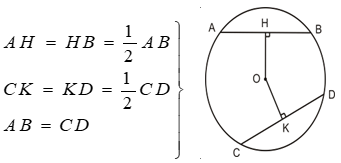
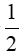 AB >
AB >