Giá trị nhỏ nhất của biểu thức F = – x + y trên miền nghiệm của hệ bất phương trình

Giải sách bài tập Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài 14 trang 30 SBT Toán 10 Tập 1: Giá trị nhỏ nhất của biểu thức F = – x + y trên miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-2x + y \le 2\\ -x + 2y \ge 4\\ x + y \le 5\end{array}\right.$.

A. 0;

B. 1;

C. 2;

D. 3.

Lời giải:

Đáp án đúng là B

Bài toán đã cho trở thành tìm nghiệm (x; y) của hệ bất phương trình $\left\{\begin{array}{l}-2x + y \le 2\\ -x + 2y \ge 4\\ x + y \le 5\end{array}\right.$ sao cho biểu thức F = – x + y đạt giá trị nhỏ nhất.

Trước hết ta xác định miền nghiệm của hệ bất phương trình đã cho:

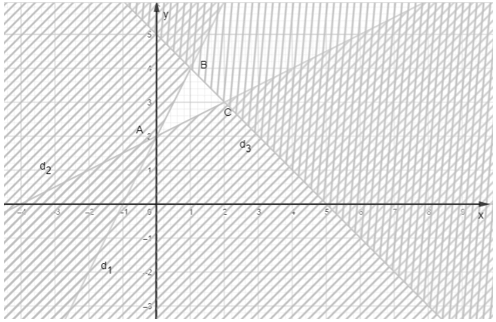
Ta có ba đường thẳng: d₁: – 2x + y = 2; d₂: – x + 2y = 4 và d₃: x + y = 5.

+) Lấy O(0; 0) có – 2.0 + 0 = 0 < 2. Do đó miền nghiệm của bất phương trình – 2x + y ≤ 2 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₁.

+) Lấy O(0; 0) có – 0 + 2.0 = 0 < 4. Do đó miền nghiệm của bất phương trình – x + 2y ≥ 4 là nửa mặt phẳng không chứa điểm O(0; 0) có bờ là đường thẳng d₂.

+) Lấy O(0; 0) có 0 + 0 = 0 < 5. Do đó miền nghiệm của bất phương trình x + y ≤ 5 là nửa mặt phẳng chứa điểm O(0; 0) và có bờ là đường thẳng d₃.

Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A(0; 2), B(1; 4) và C(2; 3) như trong hình vẽ sau:

Ta đã chứng minh được biểu thức F = – x + y có giá trị nhỏ nhất tại các đỉnh của tam giác ABC.

Tại điểm A, với x = 0, y = 2 thì F = – 0 + 2 = 2.

Tại điểm B, với x = 1, y = 4 thì F = – 1 + 4 = 3.

Tại điểm C, với x = 2, y = 3 thì F = – 2 + 3 = 1.

Vậy giá trị nhỏ nhất của biểu thức F là 1 khi x = 2 và y = 3.