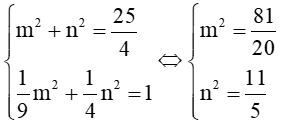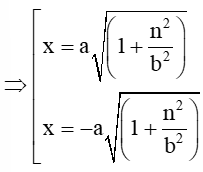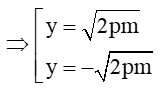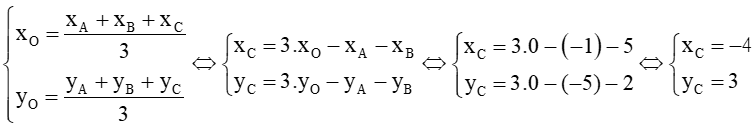Giải SBT Toán 10 trang 97 Tập 2 Cánh diều

---

Haylamdo biên soạn giải Sách bài tập Toán 10 trang 97 Tập 2 trong Bài 6: Ba đường conic SBT Toán 10 Cánh diều Tập 2 hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 97.

Giải SBT Toán 10 trang 97 Tập 2 Cánh diều

Bài 64 trang 97 SBT Toán 10 Tập 2: Phương trình nào sau đây là phương trình chính tắc của parabol?

A. y²=-0,3x;

B. x²=0,3y;

C. y²=0,3x;

D. x²=-0,3y.

Lời giải:

Phương trình chính tắc của parabol có dạng là: y²=2px (p >0)

Do đó ta thấy phương trình y²=0,3x là đúng dạng này.

Vậy chọn đáp án C.

Bài 65 trang 97 SBT Toán 10 Tập 2: Lập phương trình chính tắc của elip (E) biết (E) đi qua hai điểm P$\left(2;\frac{3\sqrt{3}}{2}\right)$ và Q$\left(2\sqrt{2};\frac{3\sqrt{2}}{2}\right)$

Lời giải:

(E) có phương trình chính tắc là: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0).

Do P thuộc (E) nên ta có:

$\frac{2^2}{a^2}+\frac{{\left(\frac{3\sqrt{3}}{2}\right)}^2}{b^2}=1\iff \frac{4}{a^2}+\frac{27}{4b^2}=1$ (1)

Do Q thuộc (E) nên ta có:

$\frac{{\left(2\sqrt{2}\right)}^2}{a^2}+\frac{{\left(\frac{3\sqrt{2}}{2}\right)}^2}{b^2}=1\iff \frac{8}{a^2}+\frac{9}{2b^2}=1$ (2)

Từ (1) và (2) ta có hệ phương trình hai ẩn $\frac{1}{a^2},\frac{1}{b^2}$:

Coi là 2 ẩn của hệ phương trình

Suy ra $\frac{1}{a^2}=\frac{1}{16};\frac{1}{b^2}=\frac{1}{9}$ $\Rightarrow$ a²=16, b²=9

Phương trình chính tắc của (E): $\frac{x^2}{16}+\frac{y^2}{9}$=1 .

Bài 66 trang 97 SBT Toán 10 Tập 2: Cho elip (E): $\frac{x^2}{9}+\frac{y^2}{4}$=1. Tìm điểm P thuộc (E) thỏa mãn OP = 2,5.

Lời giải:

Gọi điểm P có tọa độ P(m; n).

Do OP = 2,5 nên m²+n²=$\frac{25}{4}$

Do P thuộc (E) nên ta có: $\frac{1}{9}$m²+$\frac{1}{4}$n²=1

Suy ra ta có hệ phương trình

Suy ra m²=$\frac{81}{20}$; n²=$\frac{11}{5}$$\Rightarrow$m=$\pm \frac{9\sqrt{5}}{10}$; n=$\pm \frac{\sqrt{55}}{5}$.

Vậy có 4 tọa độ của điểm P:

$\left(\frac{9\sqrt{5}}{10};\frac{\sqrt{55}}{5}\right);\left(\frac{9\sqrt{5}}{10};\frac{-\sqrt{55}}{5}\right);\left(\frac{-9\sqrt{5}}{10};\frac{\sqrt{55}}{5}\right);\left(\frac{-9\sqrt{5}}{10};\frac{-\sqrt{55}}{5}\right)$.

Bài 67 trang 97 SBT Toán 10 Tập 2: Lập phương trình chính tắc của hypebol (H), biết (H) đi qua hai điểm M(- 1; 0) và N(2;2$\sqrt{3}$).

Lời giải:

Hypebol có phương trình chính tắc là: $\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1 (a>0, b>0)

Do M(-1; 0) thuộc (H) nên ta có: $\frac{{\left(-1\right)}^2}{a^2}-\frac{0^2}{b^2}$=1$\Rightarrow$a²=1

Do N(2;2$\sqrt{3}$) thuộc (H) nên ta có: $\frac{2^2}{1}-\frac{{\left(2\sqrt{3}\right)}^2}{b^2}$=1$\Rightarrow$b²=4

Suy ra phương trình chính tắc của Hypebol là: $\frac{x^2}{1}-\frac{y^2}{4}$=1.

Bài 68 trang 97 SBT Toán 10 Tập 2: Cho hypebol (H) có phương trình chính tắc: $\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1 với a > 0, b > 0 và đường thẳng y = n cắt (H) tại hai điểm P, Q phân biệt. Chứng minh hai điểm P và Q đối xứng nhau qua trục Oy.

Lời giải:

Thay y = n vào phương trình chính tắc của Parabol ta có: $\frac{x^2}{a^2}-\frac{n^2}{b^2}$=1

Suy ra x²=a².$\left(1+\frac{n^2}{b^2}\right)$

Giả sử điểm P$\left(a\sqrt{\left(1+\frac{n^2}{b^2}\right)};n\right)$ và Q$\left(-a\sqrt{\left(1+\frac{n^2}{b^2}\right)};n\right)$

Do Q và P có cùng tung độ và hoành độ đối nhau nên P và Q đối xứng nhau qua trục Oy

Bài 69 trang 97 SBT Toán 10 Tập 2: Viết phương trình chính tắc của parabol (P) biết:

a) Phương trình đường chuẩn của (P) là: x+$\frac{1}{8}$=0.

b) (P) đi qua điểm M(1; - 8).

Lời giải:

a) Gọi phương trình chính tắc của Parabol là: y²=2px (p>0)

Phương trình đường chuẩn của (P) là x+$\frac{1}{8}$=0 nên $\frac{p}{2}=\frac{1}{8}$

Suy ra p = $\frac{1}{4}$

Vậy phương trình chính tắc của (P) là: y²=$\frac{1}{2}$x.

b) Gọi phương trình chính tắc của Parabol là: y²=2px (p>0)

Do (P) đi qua điểm M(1; -8). Thay tọa độ điểm M vào phương trình chính tắc ta có: (-8)²= 2p.1 $\Rightarrow$p=32

Vậy phương trình chính tắc của (P) là:y²=64x.

Bài 70 trang 97 SBT Toán 10 Tập 2: Cho parabol (P) có phương trình chính tắc: y² = 2px (p > 0) và đường thẳng x = m (m > 0) cắt (P) tại hai điểm I, K phân biệt. Chứng minh hai điểm I và K đối xứng nhau qua trục Ox.

Lời giải:

Thay x = m vào phương trình chính tắc của Parabol ta có:

y²=2pm

Ta giả sử điểm I(m;$\sqrt{2pm}$) và điểm K(m;-$\sqrt{2pm}$)

Do I và K có cùng hoành độ và tung độ đối nhau nên I và K đối xứng nhau qua trục Ox.

Bài 71 trang 97 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho A(- 2; 1), B(1; - 3). Tọa độ của vectơ $\overrightarrow{AB}$ là:

A. (1; - 4);

B. (- 3; 4);

C. (3; - 4);

D. (1; - 2).

Lời giải:

Tọa độ của vectơ $\overrightarrow{AB}$ là:

$\overrightarrow{AB}$= (1-(-2);-3-1)= (3;-4)

Vậy chọn đáp án C.

Bài 72 trang 97 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-1; - 5), B(5; 2) và trọng tâm là gốc tọa độ. Tọa độ điểm C là:

A. (4; - 3);

B. (- 4; - 3);

C. (- 4; 3);

D. (4; 3).

Lời giải:

Do trọng tâm tam giác là gốc tọa độ nên ta có:

Suy ra tọa độ C(– 4; 3).

Vậy chọn đáp án C

Lời giải sách bài tập Toán lớp 10 Bài 6: Ba đường conic Cánh diều hay khác:

• Giải SBT Toán 10 trang 95 Tập 2

• Giải SBT Toán 10 trang 96 Tập 2

• Giải SBT Toán 10 trang 98 Tập 2

• Giải SBT Toán 10 trang 99 Tập 2