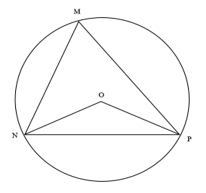
Cho tam giác MNP có MN = 10, MP = 20 và góc M = 42 độ SBT Toán 10 Tập 1

Haylamdo biên soạn và sưu tầm lời giải Bài 7 trang 75 SBT Toán 10 Tập 1 trong Bài 2: Định lí côsin và định lí sin. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Giải sách bài tập Toán 10 Bài 2: Định lí côsin và định lí sin

Bài 7 trang 75 SBT Toán 10 Tập 1: Cho tam giác MNP có MN = 10, MP = 20 và $\hat{\text{M}}$ = 42°.

a) Tính diện tích tam giác MNP.

b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP.

Lời giải:

a) Diện tích tam giác MNP là:

S = $\frac{1}{2}$.MN.MP.sin$\hat{\text{M}}$ = $\frac{1}{2}$.10.20.sin42° ≈ 67 (đvdt).

Vậy diện tích tam giác MNP là 67 đvdt.

b)

Áp dụng định lí côsin:

NP² = MP² + MN² – 2.MN.MP.cos$\hat{\text{M}}$

NP² = 10² + 20² – 2.10.20.cos42°

NP = $\sqrt{{10}^2+{20}^2–\mathrm{2.10.20.}\text{cos}42°}$

NP ≈ 14,24.

Áp dụng định lí sin trong tam giác MNP, ta có: R = ON = OP = $\frac{\text{NP}}{\text{2sin}\hat{\text{M}}}$ ≈ $\frac{14,24}{2\sin 42°}$ ≈ 10,64

Xét đường tròn tâm O ngoại tiếp tam giác MNP:

$\widehat{\text{NMP}}$ là góc nội tiếp chắn cung NP ⇒$\widehat{\text{NMP}}$= $\frac{1}{2}$$\widehat{\text{NOP}}$ ⇒ $\widehat{\text{NOP}}$ = 42°.2 = 84°.

Suy ra S_ONP = $\frac{1}{2}$.ON.OP.sin$\widehat{\text{NOP}}$ ≈ $\frac{1}{2}$.(10,64)².sin84° ≈ 56,30 (đvdt)

Vậy diện tích tam giác ONP là 56,30 đvdt.