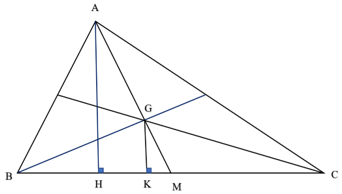
Cho tam giác ABC có trọng tâm G Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau SBT Toán 10 Tập 1

Haylamdo biên soạn và sưu tầm lời giải Bài 8 trang 75 SBT Toán 10 Tập 1 trong Bài 2: Định lí côsin và định lí sin. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Giải sách bài tập Toán 10 Bài 2: Định lí côsin và định lí sin

Bài 8 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau.

Lời giải:

Vẽ AH và GK vuông góc với BC.

Gọi M là chân đường trung tuyến từ A hạ xuống BC. Ta có GM = $\frac{1}{3}$AM ( tính chất đường trung tuyến của tam giác).

Xét tam giác GKM và tam giác AHM:

$\widehat{\text{AHM}}$ = $\widehat{\text{GKM}}$ = 90°

$\widehat{\text{AMH}}$ = $\widehat{\text{GMK}}$

⇒ tam giác GKM và tam giác AHM đồng dạng (g.g).

⇒ $\frac{\text{GM}}{\text{AM}}=\frac{\text{GK}}{\text{AH}}=\frac{1}{3}$

Có $\frac{{\text{S}}_{\text{GBC}}}{{\text{S}}_{\text{ABC}}\text{}}\text{=}\frac{\frac{\text{1}}{\text{2}}\text{.GK.BC}}{\frac{\text{1}}{\text{2}}\text{.AH.BC}}$ = $\frac{\text{GK}}{\text{AH}}=\frac{1}{3}$.

Chứng minh tương tự ta được:

S_GBC = S_GAB = S_GAC = $\frac{1}{3}$S_ABC. ( ĐPCM).