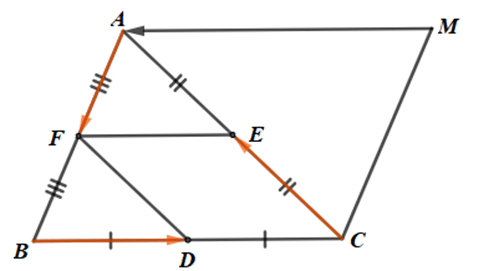
Cho tam giác ABC. Gọi D, E, F theo thứ tự là trung điểm của các cạnh BC, CA, AB

Cho tam giác ABC. Gọi D, E, F theo thứ tự là trung điểm của các cạnh BC, CA, AB.

Sách bài tập Toán 10 Kết nối tri thức Bài 8: Tổng và hiệu của hai vectơ

Bài 4.10 trang 51 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC. Gọi D, E, F theo thứ tự là trung điểm của các cạnh BC, CA, AB.

a) Xác định vectơ $\vec{A F} - \vec{B D} + \vec{C E} .$

b) Xác định điểm M thoả mãn $\vec{AF} - \vec{B D} + \vec{C E} = \vec{M A} .$

c) Chứng minh rằng $\vec{M C} = \vec{A B} .$

Lời giải:

a) Ta có: $\vec{A F} - \vec{B D} + \vec{C E}$

$= \vec{A F} + \vec{D B} + \vec{C E}$

$= \vec{A F} + \vec{D B} + \vec{E A}$ (vì E là trung điểm AC nên $\vec{C E} = \vec{E A}$ )

$= (\vec{E A} + \vec{A F}) + \vec{D B}$

$= \vec{E F} + \vec{D B}$

Vì E, F lần lượt là trung điểm của AC, AB

Nên EF là đường trung bình của tam giác ABC

$\Rightarrow$ EF // BC và $E F = \frac{1}{2} B C$

Mà D là trung điểm của BC nên $B D = \frac{1}{2} B C$

Xét tứ giác EFBD có: EF // BD, $EF = B D (= \frac{1}{2} B C)$

$\Rightarrow$ EFBD là hình bình hành

$\Rightarrow$ $\vec{E F} = \vec{D B}$

Khi đó: $\vec{A F} - \vec{B D} + \vec{C E}$ $= \vec{E F} + \vec{D B}$

$= \vec{D B} + \vec{D B}$

$= 2 \vec{D B}$

$= \vec{C B}$ (do D là trung điểm của BC)

Vậy $\vec{A F} - \vec{B D} + \vec{C E} = \vec{C B} .$

b) Điểm M thoả mãn $\vec{AF} - \vec{B D} + \vec{C E} = \vec{M A} .$

Mà $\vec{A F} - \vec{B D} + \vec{C E} = \vec{C B}$ (câu a)

Nên $\vec{M A} = \vec{C B}$

Do đó MABC là hình bình hành (theo kết quả bài tập 4.3 SGK Toán 10 tập 1)

Vậy điểm M thoả mãn tứ giác MABC là hình bình hành.

c) Vì MABC là hình bình hành (câu b)

Nên $\vec{M C} = \vec{A B}$ (theo kết quả bài tập 4.3 SGK Toán 10 tập 1)

Vậy $\vec{M C} = \vec{A B} .$