Cho hình bình hành ABCD tâm O. M là một điểm tuỳ ý thuộc cạnh BC

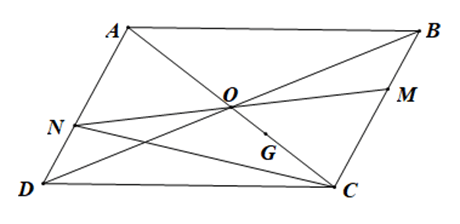
Cho hình bình hành ABCD tâm O. M là một điểm tuỳ ý thuộc cạnh BC, khác B và C. MO cắt cạnh AD tại N.

Sách bài tập Toán 10 Kết nối tri thức Bài 8: Tổng và hiệu của hai vectơ

Bài 4.8 trang 50 sách bài tập Toán lớp 10 Tập 1: Cho hình bình hành ABCD tâm O. M là một điểm tuỳ ý thuộc cạnh BC, khác B và C. MO cắt cạnh AD tại N.

a) Chứng minh rằng O là trung điểm MN.

b) Gọi G là trọng tâm tam giác BCD. Chứng minh rằng G cũng là trọng tâm tam giác MNC.

Lời giải:

a) Vì ABCD là hình bình hành tâm O

Nên O là trung điểm của AC và BD và $\widehat{ADO}=\widehat{CBO}$

Xét ∆ODN và ∆OBM có:

OD = OB (do O là trung điểm của BD),

$\widehat{DON}=\widehat{BOM}$ (hai góc đối đỉnh),

$\widehat{NDO}=\widehat{MBO}$ (do $\widehat{ADO}=\widehat{CBO}$)

$\Rightarrow$ ∆ODN = ∆OBM (g.c.g)

$\Rightarrow$ ON = OM (hai cạnh tương ứng)

$\Rightarrow$ O là trung điểm của NM.

Vậy O là trung điểm của NM.

b) Vì G là trọng tâm ∆BCD nên $\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$

$\Rightarrow \left(\overrightarrow{GM}+\overrightarrow{MB}\right)+\overrightarrow{GC}+\left(\overrightarrow{GN}+\overrightarrow{ND}\right)=\overrightarrow{0}$ (quy tắc hiệu)

$\Rightarrow \overrightarrow{GM}+\overrightarrow{MB}+\overrightarrow{GC}+\overrightarrow{GN}+\overrightarrow{ND}=\overrightarrow{0}$

$\Rightarrow \overrightarrow{GM}+\overrightarrow{GC}+\overrightarrow{GN}+\left(\overrightarrow{MB}+\overrightarrow{ND}\right)=\overrightarrow{0}$ (*)

Ta có: O là trung điểm của NM (câu a), O là trung điểm của BD (câu a)

$\Rightarrow$ BMDN là hình bình hành

$\Rightarrow \overrightarrow{BM}=\overrightarrow{ND}$$\Rightarrow -\overrightarrow{MB}=\overrightarrow{ND}$

$\Rightarrow \overrightarrow{MB}+\overrightarrow{ND}=\overrightarrow{0}$

Thay vào (*) ta được $\overrightarrow{GM}+\overrightarrow{GC}+\overrightarrow{GN}+\overrightarrow{0}=\overrightarrow{0}$

Do đó $\overrightarrow{GM}+\overrightarrow{GC}+\overrightarrow{GN}=\overrightarrow{0}$

$\Rightarrow$ G là trọng tâm tam giác MNC.

Vậy G là trọng tâm tam giác MNC.