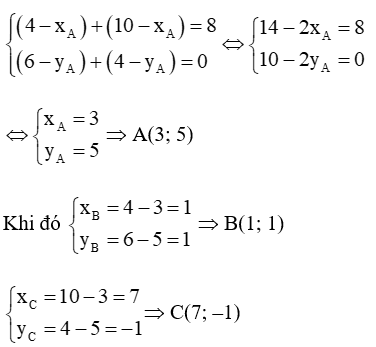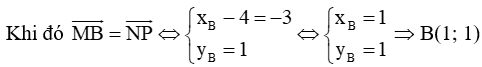Trong mặt phẳng toạ độ Oxy cho ba điểm M(4; 0), N(5; 2) và P(2, 3)

Trong mặt phẳng toạ độ Oxy cho ba điểm M(4; 0), N(5; 2) và P(2, 3). Tìm toạ độ các đỉnh của tam giác ABC, biết M, N, P theo thứ tự là trung điểm cạnh BC, CA, AB.

Sách bài tập Toán 10 Kết nối tri thức Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 4.22 trang 58 sách bài tập Toán lớp 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm M(4; 0), N(5; 2) và P(2, 3). Tìm toạ độ các đỉnh của tam giác ABC, biết M, N, P theo thứ tự là trung điểm cạnh BC, CA, AB.

Lời giải:

Cách 1:

Gọi A(x_A; y_A); B(x_B; y_B) và C(x_C; y_C) là tọa độ ba đỉnh của tam giác ABC.

Ta có:

Thay (2) và (3) vào (1) ta được:

Vậy A(3; 5), B(1; 1) và C(7; –1).

Cách 2:

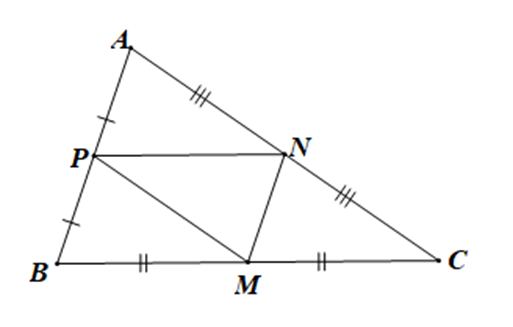
Do M, N, P lần lượt là trung điểm của BC, CA, AB

Nên MN, NP, PM là các đường trung bình của tam giác ABC.

Þ MN // AB, NP // BC, MP // AC.

+) Do MN // BM và NP // BM nên tứ giác MNPB là hình bình hành

Gọi B(x_B; y_B) và có M(4; 0), N(5; 2) và P(2, 3).

$\Rightarrow \overrightarrow{MB}=\left(x_B-4;y_B\right)$ và $\overrightarrow{NP}=\left(2-5;3-2\right)=\left(-3;1\right)$

Tương tự ta cũng có A(3; 5) và C(7; –1).

Vậy A(3; 5), B(1; 1) và C(7; –1).