Trong mặt phẳng toạ độ Oxy cho hai điểm M(–3; 2) và N(2; 7)

Trong mặt phẳng toạ độ Oxy cho hai điểm M(–3; 2) và N(2; 7).

Sách bài tập Toán 10 Kết nối tri thức Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 4.25 trang 59 sách bài tập Toán lớp 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho hai điểm M(–3; 2) và N(2; 7).

a) Tìm toạ độ của điểm P thuộc trục tung sao cho M, N, P thẳng hàng.

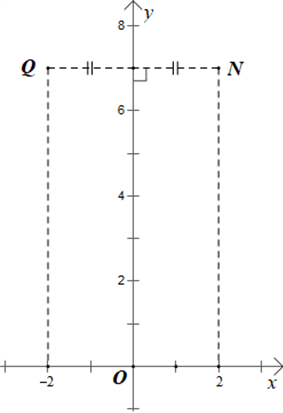
b) Tìm toạ độ của điểm Q đối xứng với N qua Oy.

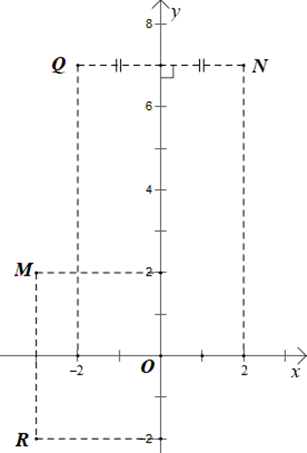
c) Tìm toạ độ của điểm R đối xứng với M qua trục hoành.

Lời giải:

a) Giả sử P(0; y_P) là điểm thuộc trục tung.

Với M(–3; 2) và N(2; 7) ta có:

$\overrightarrow{MP}=\left(3;y_P-2\right)$ và $\overrightarrow{NP}=\left(-2;y_P-7\right)$

Ba điểm M, N, P thẳng hàng

$\iff \overrightarrow{MP}$ và $\overrightarrow{NP}$ cùng phương

$\iff \frac{3}{-2}=\frac{y_P-2}{y_P-7}$ (với y_P ≠ 7)

$\iff$ 3.(y_P – 7) = –2.(y_P – 2)

$\iff$ 3.y_P – 21 = –2y_P + 4

$\iff$ 3.y_P + 2y_P = 4 + 21

$\iff$ 5.y_P = 25

$\iff$ y_P = 5 (thỏa mãn)

Vậy P(0; 5).

b)

Vì Q đối xứng với N(2; 7) qua Oy nên:

+ Hoành độ của điểm Q là số đối của hoành độ điểm N;

+ Tung độ của điểm Q bằng với tung độ của điểm N.

Do đó Q(–2; 7).

Vậy Q(–2; 7).

c)

Vì R đối xứng với M(–3; 2) qua trục hoành nên:

+ Hoành độ của điểm R bằng hoành độ điểm M;

+ Tung độ của điểm R bằng số đối của tung độ điểm M.

Do đó R(–3; –2).

Vậy R(–3; –2).