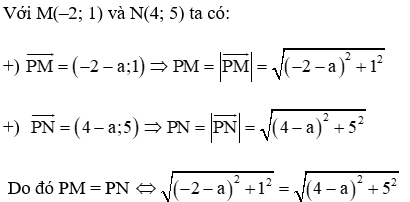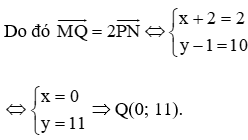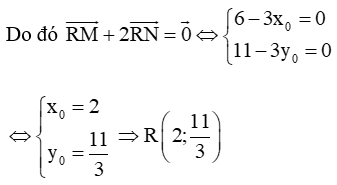Trong mặt phẳng toạ độ Oxy cho hai điểm M(–2; 1) và N(4; 5)

Trong mặt phẳng toạ độ Oxy cho hai điểm M(–2; 1) và N(4; 5).

Sách bài tập Toán 10 Kết nối tri thức Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 4.24 trang 58 sách bài tập Toán lớp 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho hai điểm M(–2; 1) và N(4; 5).

a) Tìm toạ độ của điểm P thuộc Ox sao cho PM = PN.

b) Tìm toạ độ của điểm Q sao cho $\overrightarrow{MQ}=2\overrightarrow{PN}.$

c) Tìm toạ độ của điểm R thoả mãn $\overrightarrow{RM}+2\overrightarrow{RN}=\overrightarrow{0}.$ Từ đó suy ra P, Q, R thẳng hàng.

Lời giải:

a) Gọi P(a; 0) là điểm thuộc tia Ox.

$\iff$ (–2 – a)² + 1² = (4 – a)² + 5²

$\iff$ 4 + 4a + a² + 1 = 16 – 8a + a² + 25

$\iff$ 12a = 36

$\iff$ a = 3.

Vậy P(3; 0).

b) Giả sử điểm Q có tọa độ là Q(x; y).

Với M(–2; 1), N(4; 5) và P(3; 0) ta có:

+) $\overrightarrow{MQ}=\left(x+2;y-1\right)$

+) $\overrightarrow{PN}=\left(4-3;5-0\right)=\left(1;5\right)$

$\Rightarrow 2\overrightarrow{PN}=\left(2;10\right)$

Vậy Q(0; 11).

c) Giả sử R(x₀; y₀) là điểm cần tìm.

Với M(–2; 1) và N(4; 5) ta có:

+) $\overrightarrow{RM}=\left(-2-x_0;1-y_0\right)$

+) $\overrightarrow{RN}=\left(4-x_0;5-y_0\right)$ $\Rightarrow 2\overrightarrow{RN}=\left(8-2x_0;10-2y_0\right)$

$\Rightarrow \overrightarrow{RM}+2\overrightarrow{RN}=\left(-2-x_0+8-2x_0;1-y_0+10-2y_0\right)$

+) Ta xét ba điểm: P(3; 0), Q(0; 11) và $R\left(2;\frac{11}{3}\right)$

$\Rightarrow \overrightarrow{PQ}=\left(-3;11\right)$ và $\overrightarrow{QR}=\left(2;\frac{11}{3}-11\right)=\left(2;\frac{-22}{3}\right)$

Có: $\frac{-3}{2}=\frac{11}{\frac{-22}{3}}$ nên hai vectơ $\overrightarrow{PQ}$ và $\overrightarrow{QR}$ cùng phương

Do đó P, Q, R thẳng hàng

Vậy ba điểm P, Q, R thẳng hàng.