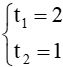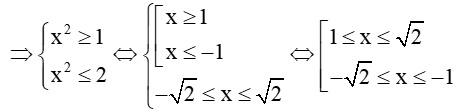Giải các bất phương trình sau: a) 3x^2 – 36x + 108 > 0

Giải các bất phương trình sau:

Sách bài tập Toán 10 Kết nối tri thức Bài 17: Dấu của tam thức bậc hai

Bài 6.22 trang 18 Sách bài tập Toán lớp 10 Tập 2: Giải các bất phương trình sau:

a) 3x² – 36x + 108 > 0;

b) –x² + 2x – 2 ≥ 0;

c) x⁴ – 3x² + 2 ≤ 0;

d) $\frac{1}{x^2-x+1}\le \frac{1}{2x^2+x+2}$.

Lời giải:

a)

Xét tam thức bậc hai f(x) = 3x² – 36x + 108 có a = 3 > 0

Phương trình bậc hai 3x² – 36x + 108 = 0 có ∆ = b² – 4ac = (–36)² – 4.3.108 = 0

Do đó, phương trình có nghiệm kép x = 6.

Do đó, f(x) = 3x² – 36x + 108 > 0 với x ∈ ℝ\{6}

Hay tập nghiệm của bất phương trình 3x² – 36x + 108 > 0 là S = ℝ\{6}.

b)

Xét tam thức bậc hai f(x) = –x² + 2x – 2 có a = –1 < 0

Phương trình bậc hai –x² + 2x – 2 = 0 có ∆ = b² – 4ac = 2² – 4.(–1).(–2) = –4 < 0

Do đó, f(x) = –x² + 2x – 2 < 0 với mọi x ∈ ℝ

Hay tập nghiệm của bất phương trình –x² + 2x – 2 ≥ 0 là S = ∅.

c)

x⁴ – 3x² + 2 ≤ 0

Đặt t = x² (t ≥ 0), khi đó, bất phương trình trở thành:

t² – 3t + 2 ≤ 0

Xét tam thức bậc hai f(t) = t² – 3t + 2 có a = 1 > 0

Phương trình bậc hai t² – 3t + 2 = 0 có ∆ = b² – 4ac = (–3)² – 4.1.2 = 1 > 0

Do đó, phương trình có hai nghiệm phân biệt là:

Do đó, f(t) = t² – 3t + 2 < 0 với t ∈ (1; 2) ⇒ t² – 3t + 2 ≤ 0 với t ∈ [1; 2] (thỏa mãn điều kiện t ≥ 0).

Ta có t ∈ [1; 2] ⇒ 1 ≤ t ≤ 2 ⇒ 1 ≤ x² ≤ 2

Hay tập nghiệm của bất phương trình x⁴ – 3x² + 2 ≤ 0 là S = [$-\sqrt{2}$;-1]$\cup$[1;$\sqrt{2}$].

d)

Xét phương trình bậc hai x² – x + 1 = 0 có a = 1 > 0 và ∆₁ = (–1)² – 4.1.1 = –3 < 0 do đó, x² – x + 1 > 0 với mọi số thực x.

Xét phương trình bậc hai 2x² + x + 2 = 0 có a = 2 > 0 và ∆₂ = 1² – 4.2.2 = –15 < 0 do đó, 2x² + x + 2 > 0 với mọi số thực x

Do đó, tập xác định của bất phương trình $\frac{1}{x^2-x+1}\le \frac{1}{2x^2+x+2}$ là D = ℝ.

Khi đó, $\frac{1}{x^2-x+1}\le \frac{1}{2x^2+x+2}$

⇔ 2x² + x + 2 ≤ x² – x + 1

⇔ x² + 2x + 1 ≤ 0

⇔ (x + 1)² ≤ 0

Do (x + 1)² ≥ 0 với mọi số thực x nên ta có:

(x + 1)² ≤ 0

⇔ (x + 1)² = 0

⇔ x + 1 = 0

⇔ x = –1

Vậy tập nghiệm của bất phương trình $\frac{1}{x^2-x+1}\le \frac{1}{2x^2+x+2}$ là S = {–1}.