Cho hai đường thẳng d: 2x + y + 1 = 0 và k: 2x + 5y – 3 = 0

Cho hai đường thẳng d: 2x + y + 1 = 0 và k: 2x + 5y – 3 = 0.

Sách bài tập Toán 10 Kết nối tri thức Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Bài 7.12 trang 38 Sách bài tập Toán lớp 10 Tập 2: Cho hai đường thẳng d: 2x + y + 1 = 0 và k: 2x + 5y – 3 = 0.

a) Chứng minh rằng hai đường thẳng cắt nhau. Tìm giao điểm của hai đường thẳng đó.

b) Tính tang của góc giữa hai đường thẳng.

Lời giải:

a)

Xét d: 2x + y + 1 = 0 và k: 2x + 5y – 3 = 0 ta có:

a₁ = 2, b₁ = 1, c₁ = 1

a₂ = 2, b₂ = 5, c₂ = –3

Xét tỉ số:

$\frac{a_1}{a_2}=\frac{2}{2}=1;\frac{b_1}{b_2}=\frac{1}{5};\frac{c_1}{c_2}=\frac{1}{-3}=\frac{-1}{3}\iff \frac{a_1}{a_2}\ne \frac{b_1}{b_2}\ne \frac{c_1}{c_2}$

Do đó, d và k cắt nhau (điều cần phải chứng minh).

Giao điểm của hai đường thẳng có tọa độ là nghiệm của hệ phương trình:

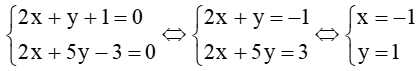
Vậy tọa độ giao điểm của hai đường thẳng là (–1; 1).

b)

Gọi φ là góc giữa hai đường thẳng d và k.

Từ giả thiết ta có $\overrightarrow{n_d}=\left(2;1\right),\overrightarrow{n_k}=\left(2;5\right)$

Do đó, theo công thức tính góc của hai đường thẳng thì:

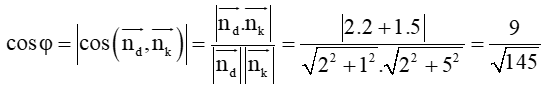
Vì φ là góc giữa hai đường thẳng nên 0° ≤ φ ≤ 90°, hơn nữa cosφ ≠ 0 và cosφ ≠ 1 nên ta có: 0° < φ < 90°, suy ra tanφ > 0.

Lại có: 1 + tan²φ = $\frac{1}{{\cos }^2\phi }$.

Do đó, ${\tan }^2\phi =\frac{1}{{\cos }^2\phi }-1=\frac{145}{81}-1=\frac{64}{81}\Rightarrow \tan \phi =\frac{8}{9}$