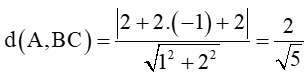Trong mặt phẳng Oxy, cho tam giác ABC có A(2; –1), B(2; –2) và C(0; –1)

Trong mặt phẳng Oxy, cho tam giác ABC có A(2; –1), B(2; –2) và C(0; –1).

Sách bài tập Toán 10 Kết nối tri thức Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Bài 7.15 trang 38 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho tam giác ABC có A(2; –1), B(2; –2) và C(0; –1).

a) Tính độ dài đường cao của tam giác ABC kẻ từ A.

b) Tính diện tích tam giác ABC.

c) Tính bán kính đường tròn nội tiếp tam giác ABC.

Lời giải:

a)

Độ dài đường cao của tam giác ABC kẻ từ A chính là khoảng cách từ điểm A đến cạnh BC.

Đường thẳng BC nhận $\overrightarrow{BC}=\left(-2;1\right)$ là một vectơ chỉ phương. Do đó $\overrightarrow{n}=\left(1;2\right)$ là một vectơ pháp tuyến của BC.

Đường thẳng BC đi qua đểm B(2; –2) và có một vectơ pháp tuyến là $\overrightarrow{n}=\left(1;2\right)$ nên có phương trình tổng quát là:

1(x – 2) + 2.[y – (–2)] = 0

⇔ x + 2y – 2 + 4 = 0

⇔ x + 2y + 2 = 0

Theo công thức tính khoảng cách, ta có

Vậy độ dài đường cao của tam giác ABC kẻ từ A là: $\frac{2}{\sqrt{5}}$ (đvđd).

b)

$\overrightarrow{BC}=\left(-2;1\right)$

Ta có $BC=\sqrt{{(-2)}^2+1^2}=\sqrt{5}$ (đvđd)

$S_{ABC}=\frac{1}{2}d(A;BC).BC=\frac{1}{2}.\frac{2}{\sqrt{5}}.\sqrt{5}=1$ (đvdt).

c)

$\overrightarrow{AB}=\left(0;-1\right)\Rightarrow AB=\sqrt{0^2+{(-1)}^2}=1$ (đvđd)

$\overrightarrow{AC}=\left(-2;0\right)\Rightarrow AC=\sqrt{{(-2)}^2+0^2}=2$ (đvđd)

$BC=\sqrt{5}$.

Vậy bán kính đường tròn nội tiếp tam giác ABC là

$r=\frac{S_{ABC}}{p}=\frac{1}{\frac{1+\sqrt{5}+2}{2}}=\frac{2}{3+\sqrt{5}}=\frac{3-\sqrt{5}}{2}$ (đvđd).