Cho đường thẳng d: x – 2y + 1 = 0 và điểm A(–2; 2)

Cho đường thẳng d: x – 2y + 1 = 0 và điểm A(–2; 2).

Sách bài tập Toán 10 Kết nối tri thức Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Bài 7.16 trang 38 Sách bài tập Toán lớp 10 Tập 2: Cho đường thẳng d: x – 2y + 1 = 0 và điểm A(–2; 2).

a) Chứng minh A không thuộc đường thẳng d.

b) Tìm toạ độ hình chiếu vuông góc của A trên đường thẳng d.

c) Xác định điểm đối xứng của A qua đường thẳng d.

Lời giải:

a)

Thay toạ độ điểm A vào phương trình đường thẳng d ta có:

–2 – 2.2 + 1 = –5 ≠ 0

Vậy điểm A không thuộc đường thẳng d (điều cần phải chứng minh).

b)

Gọi ∆ là đường thẳng đi qua A và vuông góc với đường thẳng d. Khi đó ∆ nhận vectơ chỉ phương $\overrightarrow{u_d}=\left(2;1\right)$ của đường thẳng d là một vectơ pháp tuyến nên phương trình ∆ là:

2(x + 2) + 1(y – 2) = 0

⇔ 2x + y + 4 – 2 = 0

⇔ 2x + y + 2 = 0

Hình chiếu vuông góc H của điểm A trên đường thẳng d là giao điểm của đường thẳng d và ∆. Do đó, toạ độ của điểm H là nghiệm của hệ phương trình:

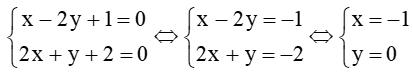
Vậy H(–1; 0).

c)

Gọi A'(x_A’; y_A’) là điểm đối xứng với A qua d. Khi đó H là trung điểm của AA’.

Ta có:

x_H = (x_A + x_A’) : 2 ⇔ x_{A’ ­­­­­­}= 2x_H – x_A = 2.(–1) – (–2) = 0

y_H = (y_A + y_A’) : 2 ⇔ y_{A’ ­­­­­­}= 2y_H – y_A = 2.0 – 2 = –2

Vậy A’(0; –2).